Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 217664 by hardmath last updated on 17/Mar/25

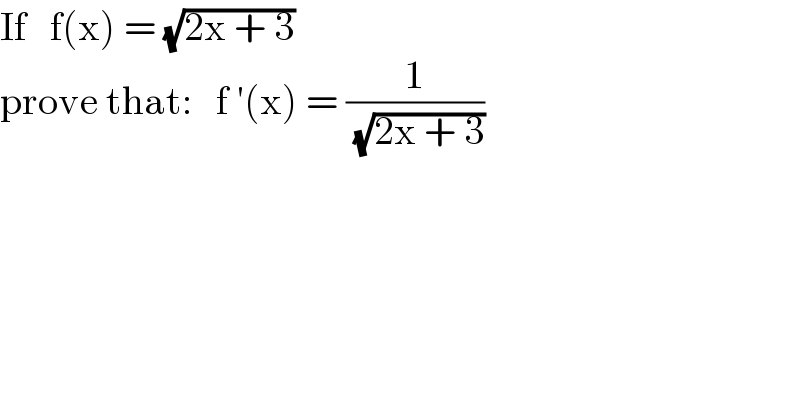
If f(x) = (√(2x + 3)) prove that: f ′(x) = (1/( (√(2x + 3))))

$$\mathrm{If}\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\sqrt{\mathrm{2x}\:+\:\mathrm{3}} \\ $$$$\mathrm{prove}\:\mathrm{that}:\:\:\:\mathrm{f}\:'\left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2x}\:+\:\mathrm{3}}}\: \\ $$

Answered by deleted50 last updated on 18/Mar/25

f^((1)) (x)=lim_(h→0) ((f(x+h)−f(x))/h). ((d )/dx)(√(2x+3))=lim_(h→0) (((√(2(x+h)+3))−(√(2x+3)))/h) lim_(h→0) (((√(2x+2h+3))−(√(2x+3)))/h)= lim_(h→0) ((((√(2x+2h+3))−(√(2x+3))))/h)∙((((√(2x+2h+3))+(√(2x+3))))/( ((√(2x+2h+3))+(√(2x+3))))) ∴lim_(h→0) ((2x+2h+3−(2x+3))/(h((√(2x+2h+3))+(√(2x+3))))) lim_(h→0) ((2x+2h+3−2x−3)/(h((√(2x+2h+3))+(√(2x+3)))))= lim_(h→0) ((2h)/(h((√(2x+h+3))+(√(2x+3))))=(2/(2(√(2x+3)))) (1/( (√(2x+3))))

$${f}^{\left(\mathrm{1}\right)} \left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}}. \\ $$$$\frac{\mathrm{d}\:\:}{\mathrm{d}{x}}\sqrt{\mathrm{2}{x}+\mathrm{3}}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}\left({x}+{h}\right)+\mathrm{3}}−\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{h}} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}−\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{h}}= \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}−\sqrt{\mathrm{2}{x}+\mathrm{3}}\right)}{{h}}\centerdot\frac{\left(\sqrt{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}+\sqrt{\mathrm{2}{x}+\mathrm{3}}\right)}{\:\left(\sqrt{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}+\sqrt{\mathrm{2}{x}+\mathrm{3}}\right)} \\ $$$$\therefore\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}−\left(\mathrm{2}{x}+\mathrm{3}\right)}{{h}\left(\sqrt{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}+\sqrt{\mathrm{2}{x}+\mathrm{3}}\right)} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\cancel{\mathrm{2}{x}}+\mathrm{2}{h}+\cancel{\mathrm{3}}−\cancel{\mathrm{2}{x}}−\cancel{\mathrm{3}}}{{h}\left(\sqrt{\mathrm{2}{x}+\mathrm{2}{h}+\mathrm{3}}+\sqrt{\mathrm{2}{x}+\mathrm{3}}\right)}= \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\cancel{{h}}}{\cancel{{h}}\left(\sqrt{\mathrm{2}{x}+{h}+\mathrm{3}}+\sqrt{\mathrm{2}{x}+\mathrm{3}}\right.}=\frac{\cancel{\mathrm{2}}}{\cancel{\mathrm{2}}\sqrt{\mathrm{2}{x}+\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{x}+\mathrm{3}}} \\ $$

Commented by hardmath last updated on 21/Mar/25

thankyou dearSir

$$\mathrm{thankyou}\:\mathrm{dearSir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com