
Question Number 182332 by mnjuly1970 last updated on 07/Dec/22
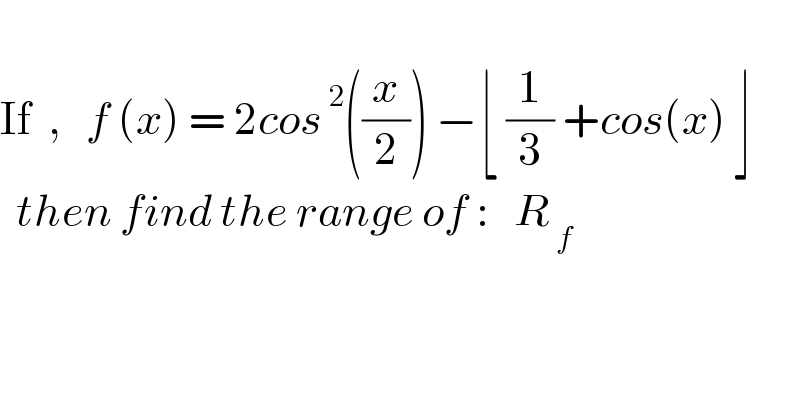
$$ \\ $$$$\mathrm{If}\:\:,\:\:\:{f}\:\left({x}\right)\:=\:\mathrm{2}{cos}^{\:\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:−\lfloor\:\frac{\mathrm{1}}{\mathrm{3}}\:+{cos}\left({x}\right)\:\rfloor \\ $$$$\:\:{then}\:{find}\:{the}\:{range}\:{of}\::\:\:\:{R}_{\:{f}} \\ $$
Answered by floor(10²Eta[1]) last updated on 07/Dec/22
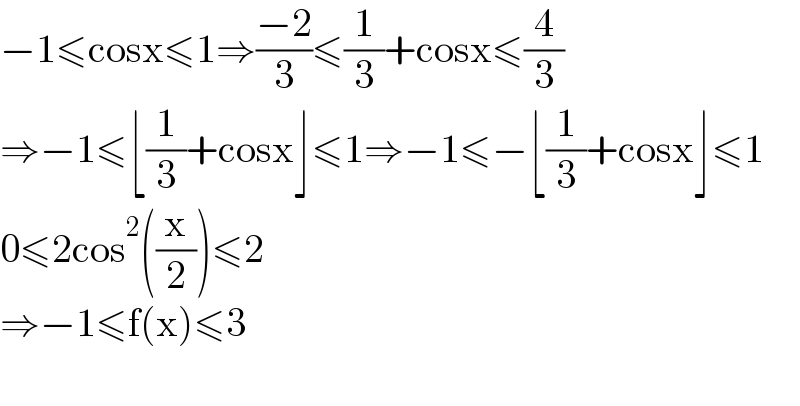
$$−\mathrm{1}\leqslant\mathrm{cosx}\leqslant\mathrm{1}\Rightarrow\frac{−\mathrm{2}}{\mathrm{3}}\leqslant\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{cosx}\leqslant\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow−\mathrm{1}\leqslant\lfloor\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{cosx}\rfloor\leqslant\mathrm{1}\Rightarrow−\mathrm{1}\leqslant−\lfloor\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{cosx}\rfloor\leqslant\mathrm{1} \\ $$$$\mathrm{0}\leqslant\mathrm{2cos}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\leqslant\mathrm{2} \\ $$$$\Rightarrow−\mathrm{1}\leqslant\mathrm{f}\left(\mathrm{x}\right)\leqslant\mathrm{3} \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 08/Dec/22
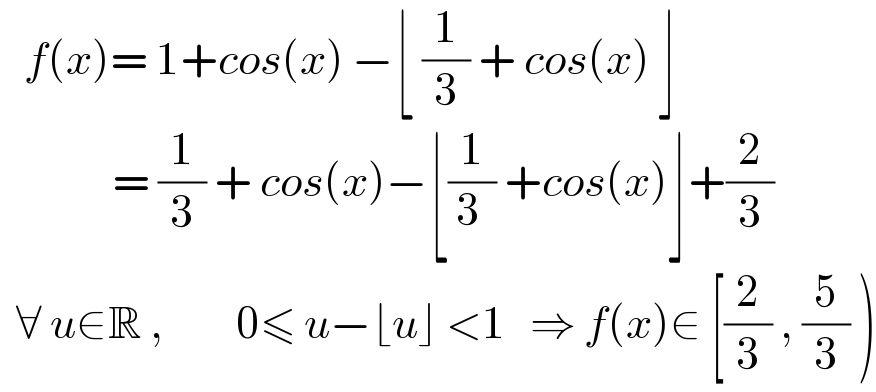
$$\:\:\:{f}\left({x}\right)=\:\mathrm{1}+{cos}\left({x}\right)\:−\lfloor\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:{cos}\left({x}\right)\:\rfloor \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:{cos}\left({x}\right)−\lfloor\frac{\mathrm{1}}{\mathrm{3}_{\:} }\:+{cos}\left({x}\right)\rfloor+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\:\:\forall\:{u}\in\mathbb{R}\:,\:\:\:\:\:\:\:\:\:\mathrm{0}\leqslant\:{u}−\lfloor{u}\rfloor\:<\mathrm{1}\:\:\:\Rightarrow\:{f}\left({x}\right)\in\:\left[\frac{\mathrm{2}}{\mathrm{3}}\:,\:\frac{\mathrm{5}}{\mathrm{3}}\:\right) \\ $$
