
Previous in Relation and Functions Next in Relation and Functions
Question Number 18859 by myintkhaing last updated on 31/Jul/17
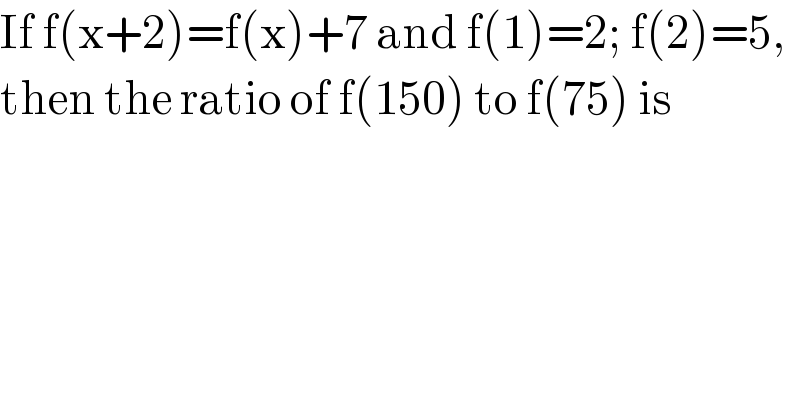
$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}+\mathrm{2}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{7}\:\mathrm{and}\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{2};\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{5}, \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{150}\right)\:\mathrm{to}\:\mathrm{f}\left(\mathrm{75}\right)\:\mathrm{is} \\ $$
Answered by 433 last updated on 31/Jul/17
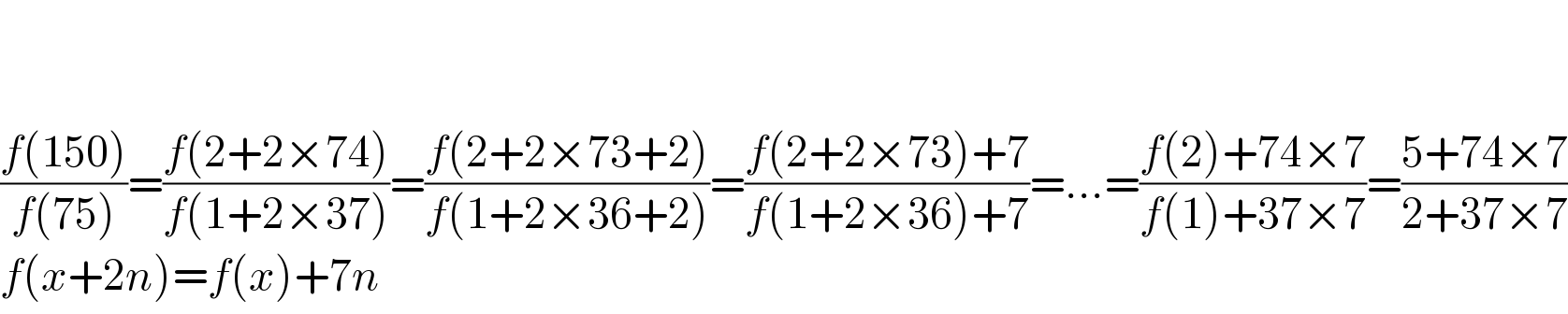
$$ \\ $$$$ \\ $$$$\frac{{f}\left(\mathrm{150}\right)}{{f}\left(\mathrm{75}\right)}=\frac{{f}\left(\mathrm{2}+\mathrm{2}×\mathrm{74}\right)}{{f}\left(\mathrm{1}+\mathrm{2}×\mathrm{37}\right)}=\frac{{f}\left(\mathrm{2}+\mathrm{2}×\mathrm{73}+\mathrm{2}\right)}{{f}\left(\mathrm{1}+\mathrm{2}×\mathrm{36}+\mathrm{2}\right)}=\frac{{f}\left(\mathrm{2}+\mathrm{2}×\mathrm{73}\right)+\mathrm{7}}{{f}\left(\mathrm{1}+\mathrm{2}×\mathrm{36}\right)+\mathrm{7}}=...=\frac{{f}\left(\mathrm{2}\right)+\mathrm{74}×\mathrm{7}}{{f}\left(\mathrm{1}\right)+\mathrm{37}×\mathrm{7}}=\frac{\mathrm{5}+\mathrm{74}×\mathrm{7}}{\mathrm{2}+\mathrm{37}×\mathrm{7}} \\ $$$${f}\left({x}+\mathrm{2}{n}\right)={f}\left({x}\right)+\mathrm{7}{n} \\ $$
