
Question Number 187311 by anurup last updated on 16/Feb/23
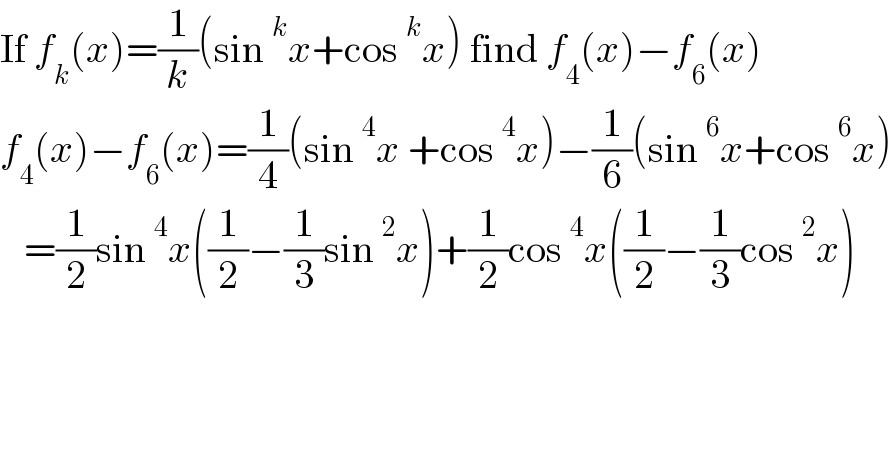
$$\mathrm{If}\:{f}_{{k}} \left({x}\right)=\frac{\mathrm{1}}{{k}}\left(\mathrm{sin}\:^{{k}} {x}+\mathrm{cos}\:^{{k}} {x}\right)\:\mathrm{find}\:{f}_{\mathrm{4}} \left({x}\right)−{f}_{\mathrm{6}} \left({x}\right) \\ $$$${f}_{\mathrm{4}} \left({x}\right)−{f}_{\mathrm{6}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{sin}\:^{\mathrm{4}} {x}\:+\mathrm{cos}\:^{\mathrm{4}} {x}\right)−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{sin}\:^{\mathrm{6}} {x}+\mathrm{cos}\:^{\mathrm{6}} {x}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{4}} {x}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:^{\mathrm{2}} {x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:^{\mathrm{4}} {x}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}\:^{\mathrm{2}} {x}\right) \\ $$
Commented by anurup last updated on 16/Feb/23
$$\mathrm{Can}\:\mathrm{anyone}\:\mathrm{help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{thi}{s} \\ $$
Commented by anurup last updated on 16/Feb/23
$$\mathrm{Can}\:\mathrm{anybody}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{how}\:\mathrm{to}\:\mathrm{proceed}\:\mathrm{further}? \\ $$
