
Question Number 207122 by MATHEMATICSAM last updated on 07/May/24
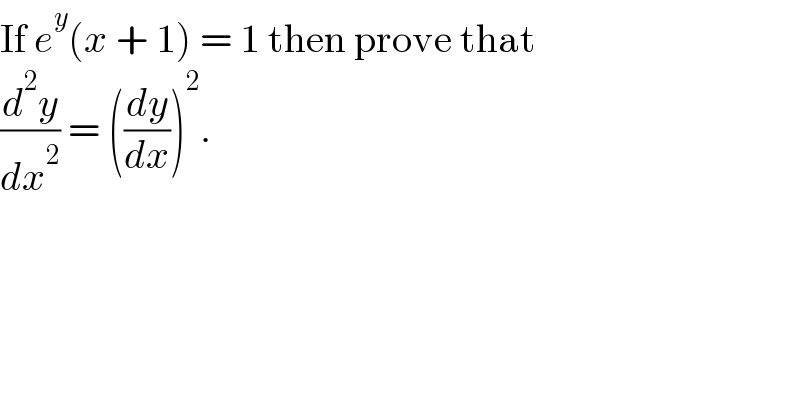
$$\mathrm{If}\:{e}^{{y}} \left({x}\:+\:\mathrm{1}\right)\:=\:\mathrm{1}\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} . \\ $$
Answered by BaliramKumar last updated on 07/May/24
![e^y = (1/(x+1)) y = −ln(x+1) (dy/dx) = −(1/(x+1)) ⇒ ((dy/dx))^2 = ((1/(x+1)))^2 (dy/dx) = −(x+1)^(−1) (d^2 y/dx^2 ) = −[−1(x+1)^(−2) ] (d^2 y/dx^2 ) = (x+1)^(−2) = ((1/(x+1)))^2 (d^2 y/dx^2 ) = ((dy/dx))^2](Q207123.png)
$$\mathrm{e}^{\mathrm{y}} \:=\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{y}\:=\:−\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\:\:\:\Rightarrow\:\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} \:=\:\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:−\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{1}} \:\:\:\:\:\:\:\:\: \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:−\left[−\mathrm{1}\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{2}} \right] \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{2}} \:=\:\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\:\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} \\ $$$$ \\ $$
