
Question Number 208791 by MATHEMATICSAM last updated on 23/Jun/24
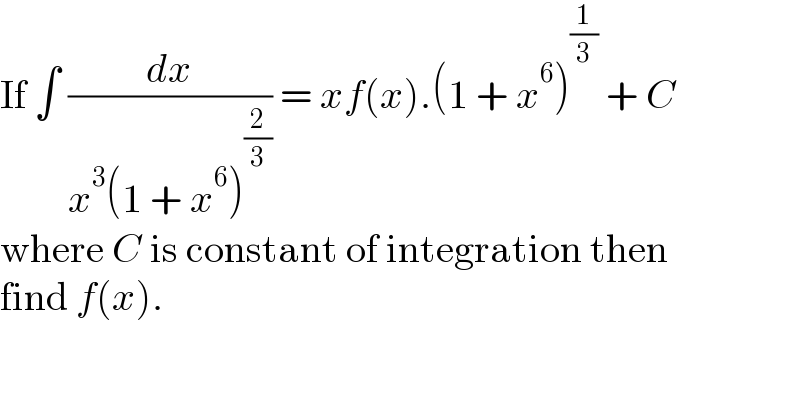
$$\mathrm{If}\:\int\:\frac{{dx}}{{x}^{\mathrm{3}} \left(\mathrm{1}\:+\:{x}^{\mathrm{6}} \right)^{\frac{\mathrm{2}}{\mathrm{3}}} }\:=\:{xf}\left({x}\right).\left(\mathrm{1}\:+\:{x}^{\mathrm{6}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:+\:{C}\: \\ $$$$\mathrm{where}\:{C}\:\mathrm{is}\:\mathrm{constant}\:\mathrm{of}\:\mathrm{integration}\:\mathrm{then} \\ $$$$\mathrm{find}\:{f}\left({x}\right). \\ $$
Commented by mr W last updated on 23/Jun/24
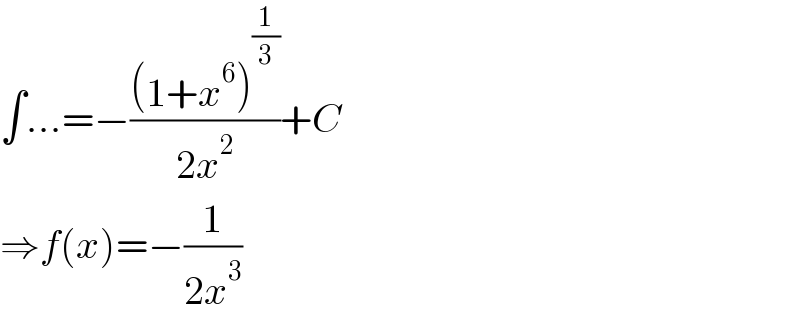
$$\int...=−\frac{\left(\mathrm{1}+{x}^{\mathrm{6}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{2}{x}^{\mathrm{2}} }+{C} \\ $$$$\Rightarrow{f}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{3}} } \\ $$
