Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188226 by Shrinava last updated on 26/Feb/23

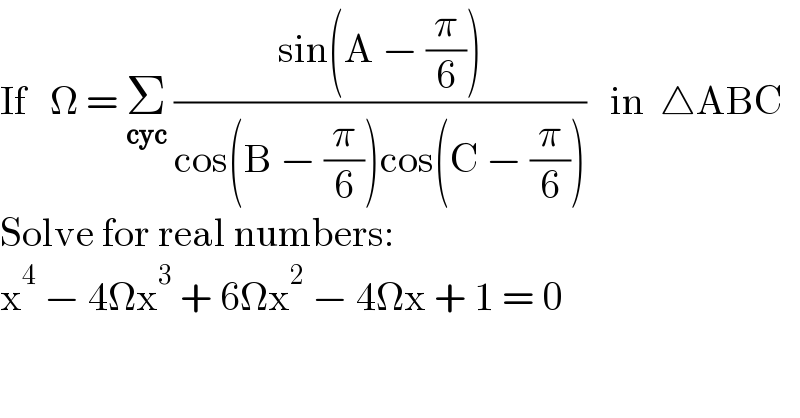
If Ω = Σ_(cyc) ((sin(A − (π/6)))/(cos(B − (π/6))cos(C − (π/6)))) in △ABC Solve for real numbers: x^4 − 4Ωx^3 + 6Ωx^2 − 4Ωx + 1 = 0

$$\mathrm{If}\:\:\:\Omega\:=\:\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\mathrm{sin}\left(\mathrm{A}\:−\:\frac{\pi}{\mathrm{6}}\right)}{\mathrm{cos}\left(\mathrm{B}\:−\:\frac{\pi}{\mathrm{6}}\right)\mathrm{cos}\left(\mathrm{C}\:−\:\frac{\pi}{\mathrm{6}}\right)}\:\:\:\mathrm{in}\:\:\bigtriangleup\mathrm{ABC} \\ $$$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{x}^{\mathrm{4}} \:−\:\mathrm{4}\Omega\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{6}\Omega\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{4}\Omega\mathrm{x}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$

Answered by aleks041103 last updated on 27/Feb/23

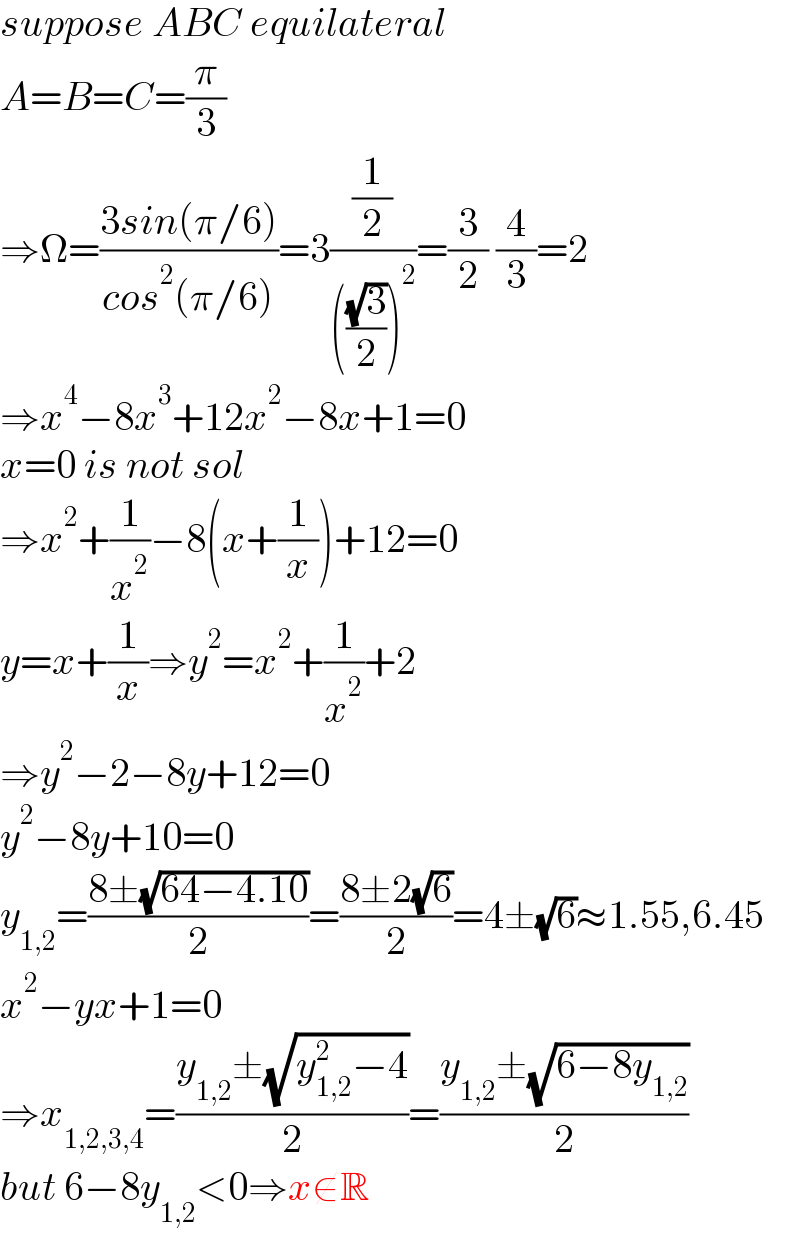
suppose ABC equilateral A=B=C=(π/3) ⇒Ω=((3sin(π/6))/(cos^2 (π/6)))=3((1/2)/((((√3)/2))^2 ))=(3/2) (4/3)=2 ⇒x^4 −8x^3 +12x^2 −8x+1=0 x=0 is not sol ⇒x^2 +(1/x^2 )−8(x+(1/x))+12=0 y=x+(1/x)⇒y^2 =x^2 +(1/x^2 )+2 ⇒y^2 −2−8y+12=0 y^2 −8y+10=0 y_(1,2) =((8±(√(64−4.10)))/2)=((8±2(√6))/2)=4±(√6)≈1.55,6.45 x^2 −yx+1=0 ⇒x_(1,2,3,4) =((y_(1,2) ±(√(y_(1,2) ^2 −4)))/2)=((y_(1,2) ±(√(6−8y_(1,2) )))/2) but 6−8y_(1,2) <0⇒x∉R

$${suppose}\:{ABC}\:{equilateral} \\ $$$${A}={B}={C}=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\Omega=\frac{\mathrm{3}{sin}\left(\pi/\mathrm{6}\right)}{{cos}^{\mathrm{2}} \left(\pi/\mathrm{6}\right)}=\mathrm{3}\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{2}}\:\frac{\mathrm{4}}{\mathrm{3}}=\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\mathrm{0}\:{is}\:{not}\:{sol} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{8}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{12}=\mathrm{0} \\ $$$${y}={x}+\frac{\mathrm{1}}{{x}}\Rightarrow{y}^{\mathrm{2}} ={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{2} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\mathrm{2}−\mathrm{8}{y}+\mathrm{12}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} −\mathrm{8}{y}+\mathrm{10}=\mathrm{0} \\ $$$${y}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{8}\pm\sqrt{\mathrm{64}−\mathrm{4}.\mathrm{10}}}{\mathrm{2}}=\frac{\mathrm{8}\pm\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{2}}=\mathrm{4}\pm\sqrt{\mathrm{6}}\approx\mathrm{1}.\mathrm{55},\mathrm{6}.\mathrm{45} \\ $$$${x}^{\mathrm{2}} −{yx}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}} =\frac{{y}_{\mathrm{1},\mathrm{2}} \pm\sqrt{{y}_{\mathrm{1},\mathrm{2}} ^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}=\frac{{y}_{\mathrm{1},\mathrm{2}} \pm\sqrt{\mathrm{6}−\mathrm{8}{y}_{\mathrm{1},\mathrm{2}} }}{\mathrm{2}} \\ $$$${but}\:\mathrm{6}−\mathrm{8}{y}_{\mathrm{1},\mathrm{2}} <\mathrm{0}\Rightarrow{x}\notin\mathbb{R} \\ $$

Commented by Shrinava last updated on 28/Feb/23

perfect dear professor thank you

$$\mathrm{perfect}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com