
Question Number 3317 by rishabh last updated on 10/Dec/15
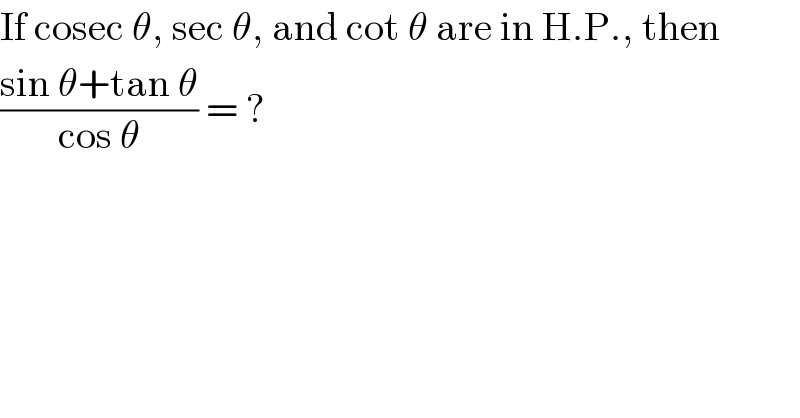
$$\mathrm{If}\:\mathrm{cosec}\:\theta,\:\mathrm{sec}\:\theta,\:\mathrm{and}\:\mathrm{cot}\:\theta\:\mathrm{are}\:\mathrm{in}\:\mathrm{H}.\mathrm{P}.,\:\mathrm{then} \\ $$$$\frac{\mathrm{sin}\:\theta+\mathrm{tan}\:\theta}{\mathrm{cos}\:\theta}\:=\:? \\ $$
Answered by prakash jain last updated on 10/Dec/15
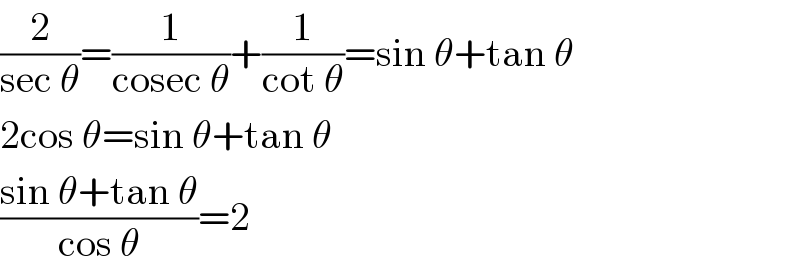
$$\frac{\mathrm{2}}{\mathrm{sec}\:\theta}=\frac{\mathrm{1}}{\mathrm{cosec}\:\theta}+\frac{\mathrm{1}}{\mathrm{cot}\:\theta}=\mathrm{sin}\:\theta+\mathrm{tan}\:\theta \\ $$$$\mathrm{2cos}\:\theta=\mathrm{sin}\:\theta+\mathrm{tan}\:\theta \\ $$$$\frac{\mathrm{sin}\:\theta+\mathrm{tan}\:\theta}{\mathrm{cos}\:\theta}=\mathrm{2} \\ $$
