Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 117482 by Don08q last updated on 12/Oct/20

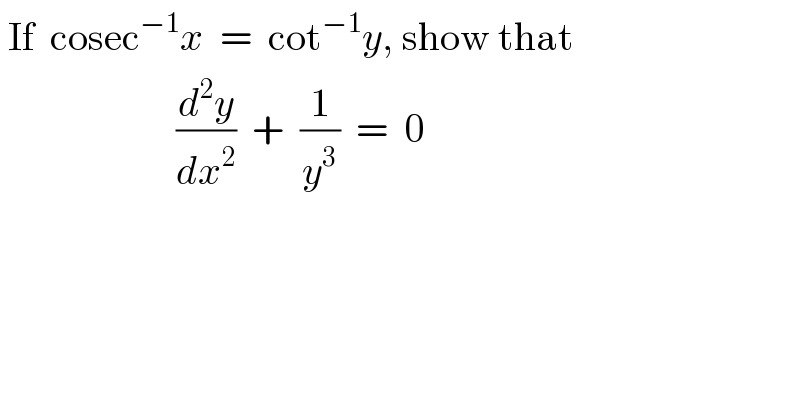
If cosec^(−1) x = cot^(−1) y, show that (d^2 y/dx^2 ) + (1/y^3 ) = 0

$$\:\mathrm{If}\:\:\mathrm{cosec}^{−\mathrm{1}} {x}\:\:=\:\:\mathrm{cot}^{−\mathrm{1}} {y},\:\mathrm{show}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:\:+\:\:\frac{\mathrm{1}}{{y}^{\mathrm{3}} }\:\:=\:\:\mathrm{0} \\ $$

Answered by TANMAY PANACEA last updated on 12/Oct/20

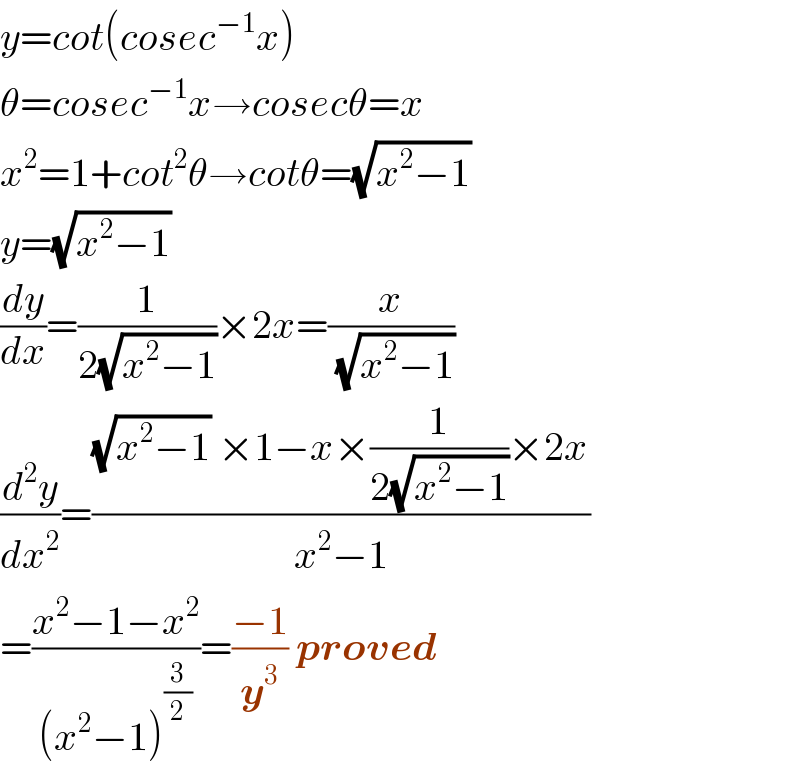
y=cot(cosec^(−1) x) θ=cosec^(−1) x→cosecθ=x x^2 =1+cot^2 θ→cotθ=(√(x^2 −1)) y=(√(x^2 −1)) (dy/dx)=(1/(2(√(x^2 −1))))×2x=(x/( (√(x^2 −1)))) (d^2 y/dx^2 )=(((√(x^2 −1)) ×1−x×(1/(2(√(x^2 −1))))×2x)/(x^2 −1)) =((x^2 −1−x^2 )/((x^2 −1)^(3/2) ))=((−1)/y^3 ) proved

$${y}={cot}\left({cosec}^{−\mathrm{1}} {x}\right) \\ $$$$\theta={cosec}^{−\mathrm{1}} {x}\rightarrow{cosec}\theta={x} \\ $$$${x}^{\mathrm{2}} =\mathrm{1}+{cot}^{\mathrm{2}} \theta\rightarrow{cot}\theta=\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\: \\ $$$${y}=\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\: \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}×\mathrm{2}{x}=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:×\mathrm{1}−{x}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}×\mathrm{2}{x}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{{x}^{\mathrm{2}} −\mathrm{1}−{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{−\mathrm{1}}{\boldsymbol{{y}}^{\mathrm{3}} }\:\boldsymbol{{proved}} \\ $$

Commented by $@y@m last updated on 12/Oct/20

Nice. I just want to add that there is no use of writing first line.

Commented by TANMAY PANACEA last updated on 13/Oct/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by Don08q last updated on 13/Oct/20

Thank you Sir

$${Thank}\:{you}\:{Sir} \\ $$

Answered by $@y@m last updated on 13/Oct/20

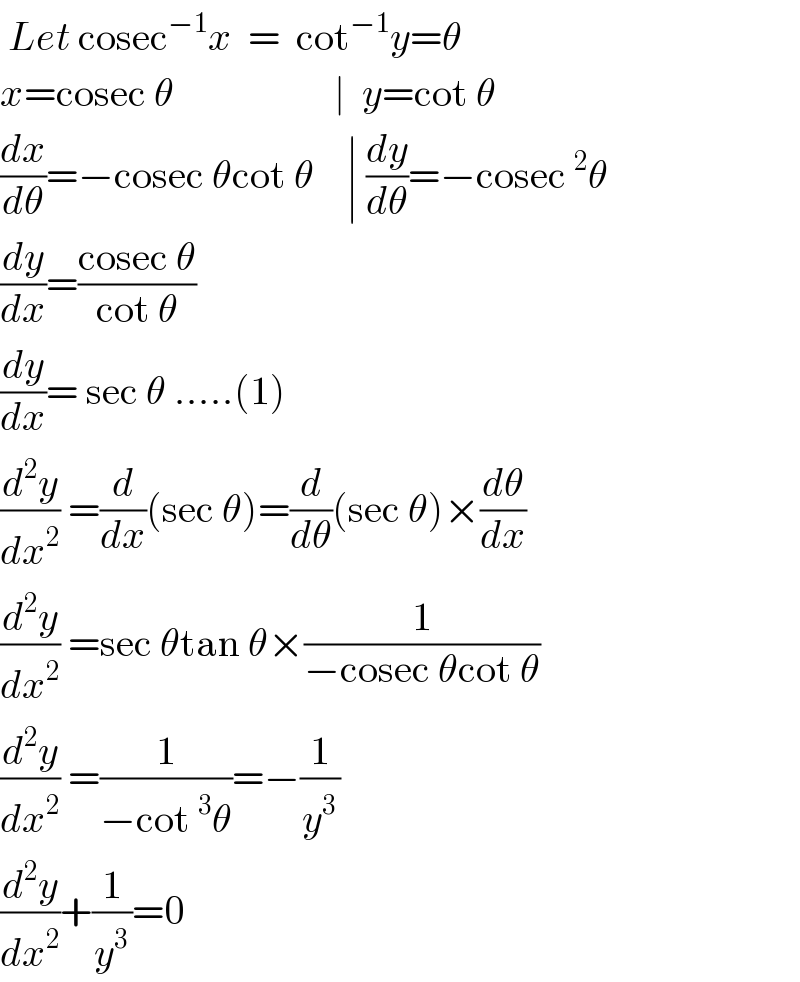
Let cosec^(−1) x = cot^(−1) y=θ x=cosec θ ∣ y=cot θ (dx/dθ)=−cosec θcot θ ∣ (dy/dθ)=−cosec^2 θ (dy/dx)=((cosec θ)/(cot θ)) (dy/dx)= sec θ .....(1) (d^2 y/dx^2 ) =(d/dx)(sec θ)=(d/dθ)(sec θ)×(dθ/dx) (d^2 y/dx^2 ) =sec θtan θ×(1/(−cosec θcot θ)) (d^2 y/dx^2 ) =(1/(−cot^3 θ))=−(1/y^3 ) (d^2 y/dx^2 )+(1/y^3 )=0

$$\:{Let}\:\mathrm{cosec}^{−\mathrm{1}} {x}\:\:=\:\:\mathrm{cot}^{−\mathrm{1}} {y}=\theta \\ $$$${x}=\mathrm{cosec}\:\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\:{y}=\mathrm{cot}\:\theta \\ $$$$\frac{{dx}}{{d}\theta}=−\mathrm{cosec}\:\theta\mathrm{cot}\:\theta\:\:\:\:\mid\:\frac{{dy}}{{d}\theta}=−\mathrm{cosec}\:^{\mathrm{2}} \theta \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{cosec}\:\theta}{\mathrm{cot}\:\theta} \\ $$$$\frac{{dy}}{{dx}}=\:\mathrm{sec}\:\theta\:.....\left(\mathrm{1}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\frac{{d}}{{dx}}\left(\mathrm{sec}\:\theta\right)=\frac{{d}}{{d}\theta}\left(\mathrm{sec}\:\theta\right)×\frac{{d}\theta}{{dx}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\mathrm{sec}\:\theta\mathrm{tan}\:\theta×\frac{\mathrm{1}}{−\mathrm{cosec}\:\theta\mathrm{cot}\:\theta} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{−\mathrm{cot}\:^{\mathrm{3}} \theta}=−\frac{\mathrm{1}}{{y}^{\mathrm{3}} } \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{\mathrm{1}}{{y}^{\mathrm{3}} }=\mathrm{0} \\ $$

Commented by Don08q last updated on 13/Oct/20

Thank you Sir

$${Thank}\:{you}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com