Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 215837 by MATHEMATICSAM last updated on 19/Jan/25

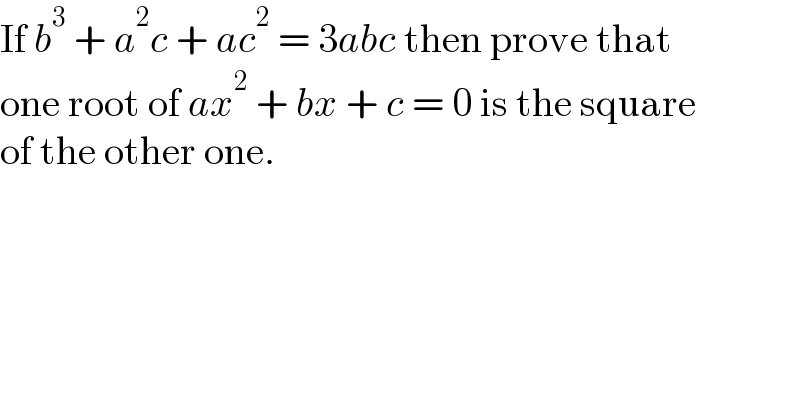
If b^3 + a^2 c + ac^2 = 3abc then prove that one root of ax^2 + bx + c = 0 is the square of the other one.

$$\mathrm{If}\:{b}^{\mathrm{3}} \:+\:{a}^{\mathrm{2}} {c}\:+\:{ac}^{\mathrm{2}} \:=\:\mathrm{3}{abc}\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{one}\:\mathrm{root}\:\mathrm{of}\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c}\:=\:\mathrm{0}\:\mathrm{is}\:\mathrm{the}\:\mathrm{square}\: \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{other}\:\mathrm{one}. \\ $$

Answered by MrGaster last updated on 19/Jan/25

given b^3 +a^2 c+ac^2 =3abc β be the roots of ax^2 +bx+c=0 by Vieta′s formulas:Σα=−(b/a)∧Πα=(c/a) if one root is the□ of the other,then ∃γ:α=γ^2 ∧β=γ∨α=γ∧β=γ^2 without loss of generality,assume α=γ^2 ∧β=γ ∴Σα=γ^2 +γ=−(b/a) Πα=γ^3 =(c/a) from beth sides by a^3 :((b/a))^3 +((c/a))+((c/a))^2 =3((b/a))((c/a)) substitute Σα and Πα:(−Σα)^3 +Πα+(Πα)^2 =3(−Σα)(Πα) (−(γ^2 +γ))^3 +γ^3 +(γ^3 )^2 =3(−(γ^2 +γ))(γ^3 ) −3γ^4 =−3γ^4 bx+c=0 is indeed the □ of the other. ps:“□” denotes squaring.

$$\mathrm{given}\:{b}^{\mathrm{3}} +{a}^{\mathrm{2}} {c}+{ac}^{\mathrm{2}} =\mathrm{3}{abc} \\ $$$$\beta\:{be}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$$\mathrm{by}\:\mathrm{Vieta}'{s}\:\mathrm{formulas}:\Sigma\alpha=−\frac{{b}}{{a}}\wedge\Pi\alpha=\frac{{c}}{{a}} \\ $$$$\mathrm{if}\:\mathrm{one}\:\mathrm{root}\:\mathrm{is}\:\mathrm{the}\Box\:\mathrm{of}\:\mathrm{the}\:\mathrm{other},\mathrm{then}\:\exists\gamma:\alpha=\gamma^{\mathrm{2}} \wedge\beta=\gamma\vee\alpha=\gamma\wedge\beta=\gamma^{\mathrm{2}} \\ $$$$\mathrm{without}\:\mathrm{loss}\:\mathrm{of}\:\mathrm{generality},\mathrm{assume}\:\alpha=\gamma^{\mathrm{2}} \wedge\beta=\gamma \\ $$$$\therefore\Sigma\alpha=\gamma^{\mathrm{2}} +\gamma=−\frac{{b}}{{a}} \\ $$$$\Pi\alpha=\gamma^{\mathrm{3}} =\frac{{c}}{{a}} \\ $$$$\mathrm{from}\:\mathrm{beth}\:\mathrm{sides}\:\mathrm{by}\:{a}^{\mathrm{3}} :\left(\frac{{b}}{{a}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{c}}{{a}}\right)+\left(\frac{\mathrm{c}}{{a}}\right)^{\mathrm{2}} =\mathrm{3}\left(\frac{{b}}{{a}}\right)\left(\frac{{c}}{{a}}\right) \\ $$$$\mathrm{substitute}\:\Sigma\alpha\:\mathrm{and}\:\Pi\alpha:\left(−\Sigma\alpha\right)^{\mathrm{3}} +\Pi\alpha+\left(\Pi\alpha\right)^{\mathrm{2}} =\mathrm{3}\left(−\Sigma\alpha\right)\left(\Pi\alpha\right) \\ $$$$\left(−\left(\gamma^{\mathrm{2}} +\gamma\right)\right)^{\mathrm{3}} +\gamma^{\mathrm{3}} +\left(\gamma^{\mathrm{3}} \right)^{\mathrm{2}} =\mathrm{3}\left(−\left(\gamma^{\mathrm{2}} +\gamma\right)\right)\left(\gamma^{\mathrm{3}} \right) \\ $$$$−\mathrm{3}\gamma^{\mathrm{4}} =−\mathrm{3}\gamma^{\mathrm{4}} \\ $$$${bx}+{c}=\mathrm{0}\:\mathrm{is}\:\mathrm{indeed}\:\mathrm{the}\:\Box\:\mathrm{of}\:\mathrm{the}\:\mathrm{other}. \\ $$$$\mathrm{ps}:``\Box''\:\:\mathrm{denotes}\:\mathrm{squaring}. \\ $$

Commented by A5T last updated on 19/Jan/25

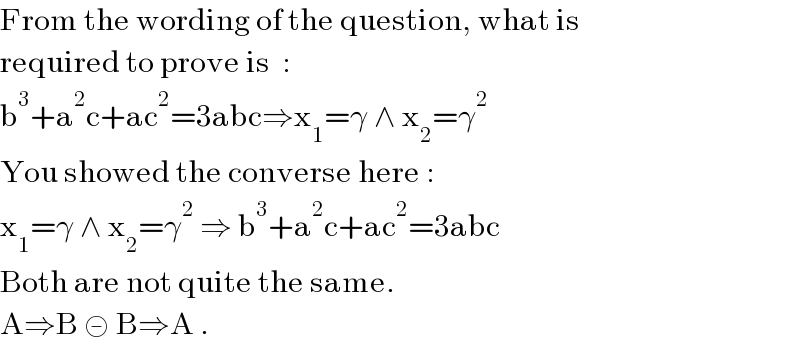
From the wording of the question, what is required to prove is : b^3 +a^2 c+ac^2 =3abc⇒x_1 =γ ∧ x_2 =γ^2 You showed the converse here : x_1 =γ ∧ x_2 =γ^2 ⇒ b^3 +a^2 c+ac^2 =3abc Both are not quite the same. A⇒B ≢ B⇒A .

$$\mathrm{From}\:\mathrm{the}\:\mathrm{wording}\:\mathrm{of}\:\mathrm{the}\:\mathrm{question},\:\mathrm{what}\:\mathrm{is}\: \\ $$$$\mathrm{required}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{is}\:\::\: \\ $$$$\mathrm{b}^{\mathrm{3}} +\mathrm{a}^{\mathrm{2}} \mathrm{c}+\mathrm{ac}^{\mathrm{2}} =\mathrm{3abc}\Rightarrow\mathrm{x}_{\mathrm{1}} =\gamma\:\wedge\:\mathrm{x}_{\mathrm{2}} =\gamma^{\mathrm{2}} \\ $$$$\mathrm{You}\:\mathrm{showed}\:\mathrm{the}\:\mathrm{converse}\:\mathrm{here}\:: \\ $$$$\mathrm{x}_{\mathrm{1}} =\gamma\:\wedge\:\mathrm{x}_{\mathrm{2}} =\gamma^{\mathrm{2}} \:\Rightarrow\:\mathrm{b}^{\mathrm{3}} +\mathrm{a}^{\mathrm{2}} \mathrm{c}+\mathrm{ac}^{\mathrm{2}} =\mathrm{3abc}\:\: \\ $$$$\mathrm{Both}\:\mathrm{are}\:\mathrm{not}\:\mathrm{quite}\:\mathrm{the}\:\mathrm{same}. \\ $$$$\mathrm{A}\Rightarrow\mathrm{B}\:≢\:\mathrm{B}\Rightarrow\mathrm{A}\:. \\ $$

Answered by A5T last updated on 19/Jan/25

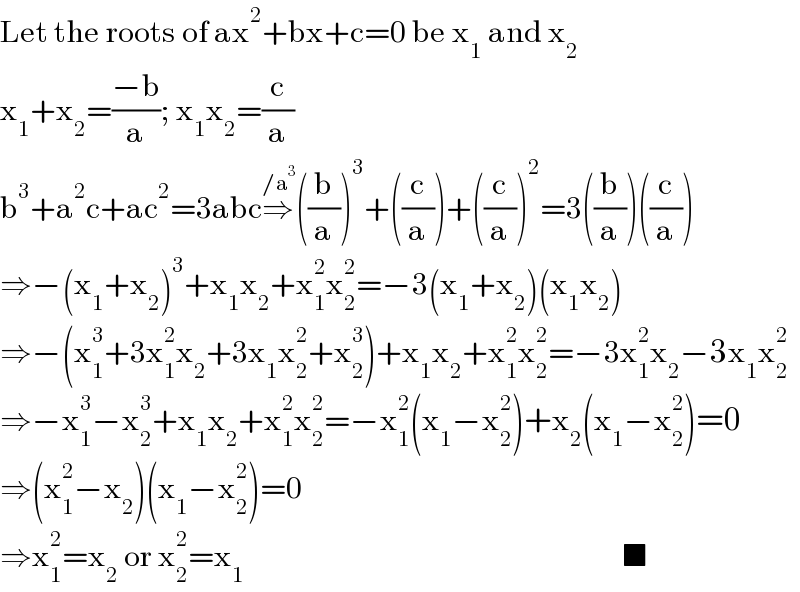
Let the roots of ax^2 +bx+c=0 be x_1 and x_2 x_1 +x_2 =((−b)/a); x_1 x_2 =(c/a) b^3 +a^2 c+ac^2 =3abc⇒^(/a^3 ) ((b/a))^3 +((c/a))+((c/a))^2 =3((b/a))((c/a)) ⇒−(x_1 +x_2 )^3 +x_1 x_2 +x_1 ^2 x_2 ^2 =−3(x_1 +x_2 )(x_1 x_2 ) ⇒−(x_1 ^3 +3x_1 ^2 x_2 +3x_1 x_2 ^2 +x_2 ^3 )+x_1 x_2 +x_1 ^2 x_2 ^2 =−3x_1 ^2 x_2 −3x_1 x_2 ^2 ⇒−x_1 ^3 −x_2 ^3 +x_1 x_2 +x_1 ^2 x_2 ^2 =−x_1 ^2 (x_1 −x_2 ^2 )+x_2 (x_1 −x_2 ^2 )=0 ⇒(x_1 ^2 −x_2 )(x_1 −x_2 ^2 )=0 ⇒x_1 ^2 =x_2 or x_2 ^2 =x_1 ■

$$\mathrm{Let}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}=\mathrm{0}\:\mathrm{be}\:\mathrm{x}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} \\ $$$$\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{b}}{\mathrm{a}};\:\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} =\frac{\mathrm{c}}{\mathrm{a}} \\ $$$$\mathrm{b}^{\mathrm{3}} +\mathrm{a}^{\mathrm{2}} \mathrm{c}+\mathrm{ac}^{\mathrm{2}} =\mathrm{3abc}\overset{/\mathrm{a}^{\mathrm{3}} } {\Rightarrow}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{c}}{\mathrm{a}}\right)+\left(\frac{\mathrm{c}}{\mathrm{a}}\right)^{\mathrm{2}} =\mathrm{3}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\left(\frac{\mathrm{c}}{\mathrm{a}}\right) \\ $$$$\Rightarrow−\left(\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} \right)^{\mathrm{3}} +\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} =−\mathrm{3}\left(\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} \right)\left(\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} \right) \\ $$$$\Rightarrow−\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{3x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} +\mathrm{3x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{x}_{\mathrm{2}} ^{\mathrm{3}} \right)+\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} =−\mathrm{3x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} −\mathrm{3x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\Rightarrow−\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{x}_{\mathrm{2}} ^{\mathrm{3}} +\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} =−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{x}_{\mathrm{1}} −\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} \right)+\mathrm{x}_{\mathrm{2}} \left(\mathrm{x}_{\mathrm{1}} −\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{x}_{\mathrm{2}} \right)\left(\mathrm{x}_{\mathrm{1}} −\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{x}_{\mathrm{2}} \:\mathrm{or}\:\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{x}_{\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$

Commented by ArshadS last updated on 19/Jan/25

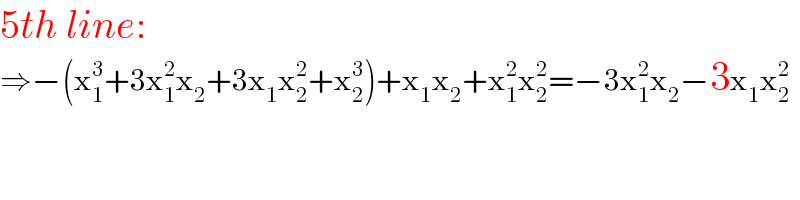
5th line: ⇒−(x_1 ^3 +3x_1 ^2 x_2 +3x_1 x_2 ^2 +x_2 ^3 )+x_1 x_2 +x_1 ^2 x_2 ^2 =−3x_1 ^2 x_2 −3x_1 x_2 ^2

$$\mathrm{5}{th}\:{line}: \\ $$$$\Rightarrow−\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{3x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} +\mathrm{3x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{x}_{\mathrm{2}} ^{\mathrm{3}} \right)+\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} =−\mathrm{3x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} −\mathrm{3x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} \\ $$

Commented by A5T last updated on 19/Jan/25

It was a typo, thanks.

$$\mathrm{It}\:\mathrm{was}\:\mathrm{a}\:\mathrm{typo},\:\mathrm{thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com