
Question Number 205353 by MATHEMATICSAM last updated on 17/Mar/24
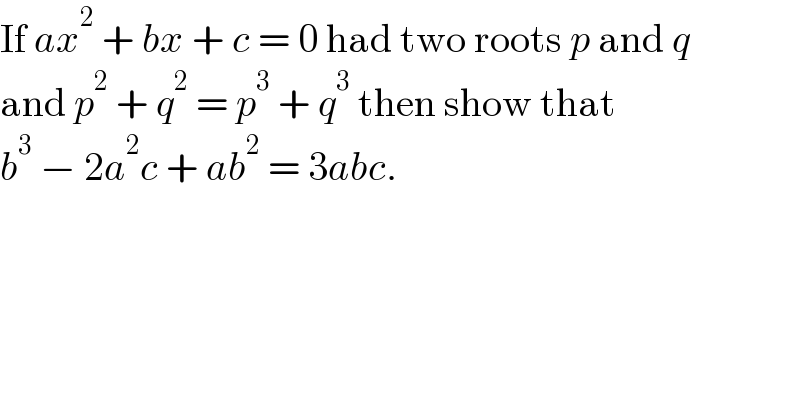
$$\mathrm{If}\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c}\:=\:\mathrm{0}\:\mathrm{had}\:\mathrm{two}\:\mathrm{roots}\:{p}\:\mathrm{and}\:{q} \\ $$$$\mathrm{and}\:{p}^{\mathrm{2}} \:+\:{q}^{\mathrm{2}} \:=\:{p}^{\mathrm{3}} \:+\:{q}^{\mathrm{3}} \:\mathrm{then}\:\mathrm{show}\:\mathrm{that} \\ $$$${b}^{\mathrm{3}} \:−\:\mathrm{2}{a}^{\mathrm{2}} {c}\:+\:{ab}^{\mathrm{2}} \:=\:\mathrm{3}{abc}. \\ $$
Answered by sniper237 last updated on 17/Mar/24
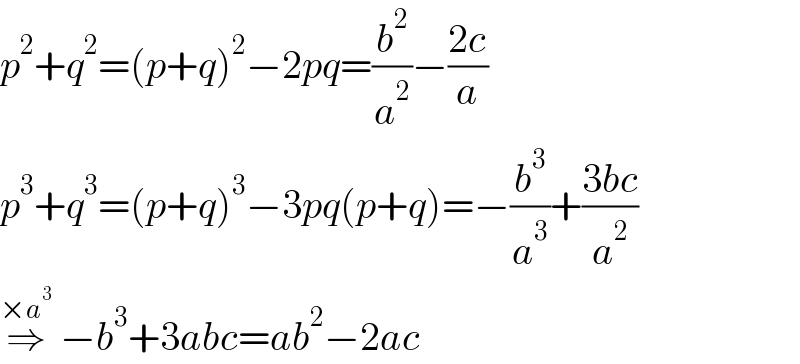
$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}{pq}=\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{\mathrm{2}{c}}{{a}} \\ $$$${p}^{\mathrm{3}} +{q}^{\mathrm{3}} =\left({p}+{q}\right)^{\mathrm{3}} −\mathrm{3}{pq}\left({p}+{q}\right)=−\frac{{b}^{\mathrm{3}} }{{a}^{\mathrm{3}} }+\frac{\mathrm{3}{bc}}{{a}^{\mathrm{2}} } \\ $$$$\overset{×{a}^{\mathrm{3}} } {\Rightarrow}\:−{b}^{\mathrm{3}} +\mathrm{3}{abc}={ab}^{\mathrm{2}} −\mathrm{2}{ac} \\ $$
Answered by A5T last updated on 17/Mar/24
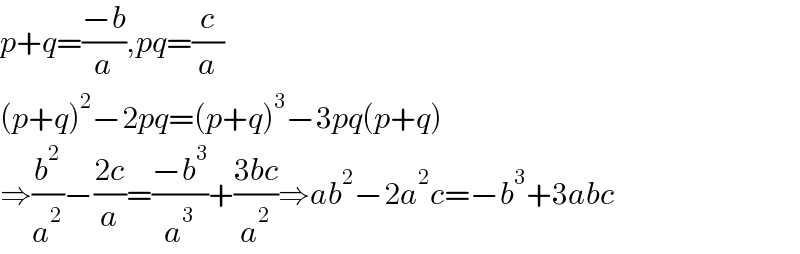
$${p}+{q}=\frac{−{b}}{{a}},{pq}=\frac{{c}}{{a}} \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}{pq}=\left({p}+{q}\right)^{\mathrm{3}} −\mathrm{3}{pq}\left({p}+{q}\right) \\ $$$$\Rightarrow\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{\mathrm{2}{c}}{{a}}=\frac{−{b}^{\mathrm{3}} }{{a}^{\mathrm{3}} }+\frac{\mathrm{3}{bc}}{{a}^{\mathrm{2}} }\Rightarrow{ab}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} {c}=−{b}^{\mathrm{3}} +\mathrm{3}{abc} \\ $$
