Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 216421 by MATHEMATICSAM last updated on 07/Feb/25

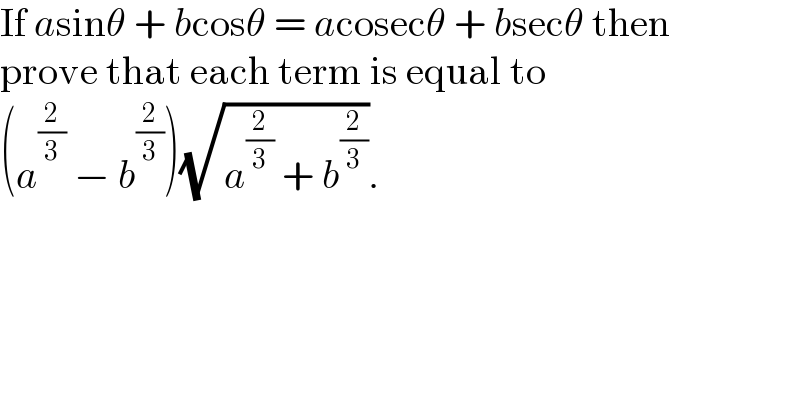
If asinθ + bcosθ = acosecθ + bsecθ then prove that each term is equal to (a^(2/3) − b^(2/3) )(√(a^(2/3) + b^(2/3) )).

$$\mathrm{If}\:{a}\mathrm{sin}\theta\:+\:{b}\mathrm{cos}\theta\:=\:{a}\mathrm{cosec}\theta\:+\:{b}\mathrm{sec}\theta\:\mathrm{then} \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{each}\:\mathrm{term}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\left({a}^{\frac{\mathrm{2}}{\mathrm{3}}} \:−\:{b}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)\sqrt{{a}^{\frac{\mathrm{2}}{\mathrm{3}}} \:+\:{b}^{\frac{\mathrm{2}}{\mathrm{3}}} }. \\ $$

Answered by mr W last updated on 07/Feb/25

a sin θ+b cos θ=(a/(sin θ))+(b/(cos θ))=k, say a sin θ+b cos θ=k ...(i) a cos θ+b sin θ=k sin θ cos θ ...(ii) a cos θ+b sin θ=(a sin θ+b cos θ) sin θ cos θ a cos θ(1−sin^2 θ)+b sin θ (1−cos^2 θ)=0 a cos^3 θ+b sin^3 θ=0 ⇒tan θ=−(a^(1/3) /b^(1/3) ) ⇒sin θ=±(a^(1/3) /( (√(a^(2/3) +b^(2/3) )))) ⇒cos θ=∓(b^(1/3) /( (√(a^(2/3) +b^(2/3) )))) k=(a/(sin θ))+(b/(cos θ)) =±(a^(2/3) −b^(2/3) )(√(a^(2/3) +b^(2/3) )) ✓

$${a}\:\mathrm{sin}\:\theta+{b}\:\mathrm{cos}\:\theta=\frac{{a}}{\mathrm{sin}\:\theta}+\frac{{b}}{\mathrm{cos}\:\theta}={k},\:{say} \\ $$$${a}\:\mathrm{sin}\:\theta+{b}\:\mathrm{cos}\:\theta={k}\:\:\:...\left({i}\right) \\ $$$${a}\:\mathrm{cos}\:\theta+{b}\:\mathrm{sin}\:\theta={k}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:\:...\left({ii}\right) \\ $$$${a}\:\mathrm{cos}\:\theta+{b}\:\mathrm{sin}\:\theta=\left({a}\:\mathrm{sin}\:\theta+{b}\:\mathrm{cos}\:\theta\right)\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$${a}\:\mathrm{cos}\:\theta\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\theta\right)+{b}\:\mathrm{sin}\:\theta\:\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)=\mathrm{0} \\ $$$${a}\:\mathrm{cos}^{\mathrm{3}} \:\theta+{b}\:\mathrm{sin}^{\mathrm{3}} \:\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=−\frac{{a}^{\frac{\mathrm{1}}{\mathrm{3}}} }{{b}^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\pm\frac{{a}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\:\sqrt{{a}^{\frac{\mathrm{2}}{\mathrm{3}}} +{b}^{\frac{\mathrm{2}}{\mathrm{3}}} }} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\mp\frac{{b}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\:\sqrt{{a}^{\frac{\mathrm{2}}{\mathrm{3}}} +{b}^{\frac{\mathrm{2}}{\mathrm{3}}} }} \\ $$$${k}=\frac{{a}}{\mathrm{sin}\:\theta}+\frac{{b}}{\mathrm{cos}\:\theta} \\ $$$$\:\:\:=\pm\left({a}^{\frac{\mathrm{2}}{\mathrm{3}}} −{b}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)\sqrt{{a}^{\frac{\mathrm{2}}{\mathrm{3}}} +{b}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:\:\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com