
Question Number 206471 by MATHEMATICSAM last updated on 15/Apr/24
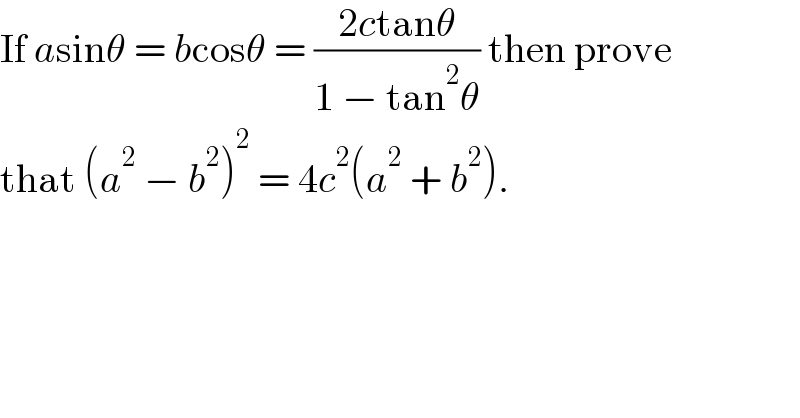
$$\mathrm{If}\:{a}\mathrm{sin}\theta\:=\:{b}\mathrm{cos}\theta\:=\:\frac{\mathrm{2}{c}\mathrm{tan}\theta}{\mathrm{1}\:−\:\mathrm{tan}^{\mathrm{2}} \theta}\:\mathrm{then}\:\mathrm{prove} \\ $$$$\mathrm{that}\:\left({a}^{\mathrm{2}} \:−\:{b}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\:\mathrm{4}{c}^{\mathrm{2}} \left({a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \right). \\ $$
Answered by lepuissantcedricjunior last updated on 15/Apr/24
![asin𝛉=((2c tan𝛉)/(1−tan^2 𝛉))=ctan2𝛉=((2csin𝛉cos𝛉)/(2cos^2 𝛉−1))=bcos𝛉 ⇔a=((2ccos𝛉)/(2cos^2 𝛉−1));b=((2csin𝛉)/(2cos^2 𝛉−1)) on a (a^2 −b^2 )^2 =(((4c^2 cos2𝛉)/((2cos^2 𝛉−1)^2 )))^2 =16c^4 (((cos2𝛉)/(cos^2 (2𝛉))))^2 ⇒(a^2 −b^2 )^2 =16c^4 ((1/(cos^2 (2𝛉)))) =16c^4 [(1/(4c^2 )) (((4c^2 sin^2 𝛉)/(cos^2 (2𝛉)))+((4c^2 cos^2 𝛉)/(cos^2 (2𝛉))) )] =4c^2 (a^2 +b^2 ) ⇒(a^2 −b^2 )^2 =4c^2 (a^2 +b^2 ) .........le puissant cedric junior.....](Q206472.png)
$$\boldsymbol{{asin}\theta}=\frac{\mathrm{2}\boldsymbol{{c}}\:\boldsymbol{{tan}\theta}}{\mathrm{1}−\boldsymbol{{tan}}^{\mathrm{2}} \boldsymbol{\theta}}=\boldsymbol{{ctan}}\mathrm{2}\boldsymbol{\theta}=\frac{\mathrm{2}\boldsymbol{{csin}\theta{cos}\theta}}{\mathrm{2}\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\theta}−\mathrm{1}}=\boldsymbol{{bcos}\theta} \\ $$$$\Leftrightarrow\boldsymbol{{a}}=\frac{\mathrm{2}\boldsymbol{{ccos}\theta}}{\mathrm{2}\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\theta}−\mathrm{1}};\boldsymbol{{b}}=\frac{\mathrm{2}\boldsymbol{{csin}\theta}}{\mathrm{2}\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\theta}−\mathrm{1}} \\ $$$$\boldsymbol{{on}}\:\boldsymbol{{a}}\: \\ $$$$\left(\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} \right)^{\mathrm{2}} =\left(\frac{\mathrm{4}\boldsymbol{{c}}^{\mathrm{2}} \boldsymbol{{cos}}\mathrm{2}\boldsymbol{\theta}}{\left(\mathrm{2}\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\theta}−\mathrm{1}\right)^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{16}\boldsymbol{{c}}^{\mathrm{4}} \left(\frac{\boldsymbol{{cos}}\mathrm{2}\boldsymbol{\theta}}{\boldsymbol{{cos}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\theta}\right)}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{16}\boldsymbol{{c}}^{\mathrm{4}} \left(\frac{\mathrm{1}}{\boldsymbol{{cos}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\theta}\right)}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{16}\boldsymbol{{c}}^{\mathrm{4}} \left[\frac{\mathrm{1}}{\mathrm{4}\boldsymbol{{c}}^{\mathrm{2}} }\:\left(\frac{\mathrm{4}\boldsymbol{{c}}^{\mathrm{2}} \boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{\theta}}{\boldsymbol{{cos}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\theta}\right)}+\frac{\mathrm{4}\boldsymbol{{c}}^{\mathrm{2}} \boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\theta}}{\boldsymbol{{cos}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\theta}\right)}\:\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}\boldsymbol{{c}}^{\mathrm{2}} \left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\left(\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}\boldsymbol{{c}}^{\mathrm{2}} \left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} \right) \\ $$$$.........\boldsymbol{{le}}\:\boldsymbol{{puissant}}\:\boldsymbol{{cedric}}\:\boldsymbol{{junior}}..... \\ $$$$ \\ $$$$ \\ $$
