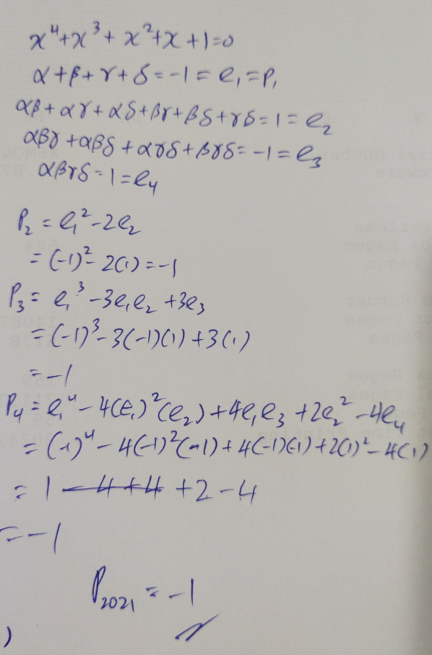Question Number 215811 by MATHEMATICSAM last updated on 18/Jan/25
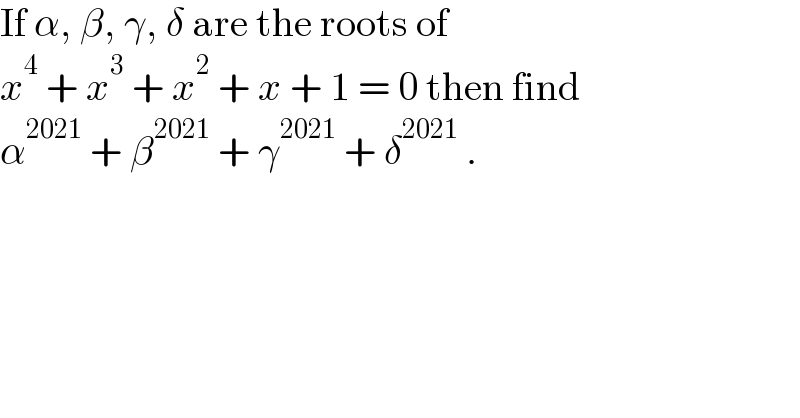
$$\mathrm{If}\:\alpha,\:\beta,\:\gamma,\:\delta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\: \\ $$$${x}^{\mathrm{4}} \:+\:{x}^{\mathrm{3}} \:+\:{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\:=\:\mathrm{0}\:\mathrm{then}\:\mathrm{find} \\ $$$$\alpha^{\mathrm{2021}} \:+\:\beta^{\mathrm{2021}} \:+\:\gamma^{\mathrm{2021}} \:+\:\delta^{\mathrm{2021}} \:. \\ $$
Answered by A5T last updated on 18/Jan/25
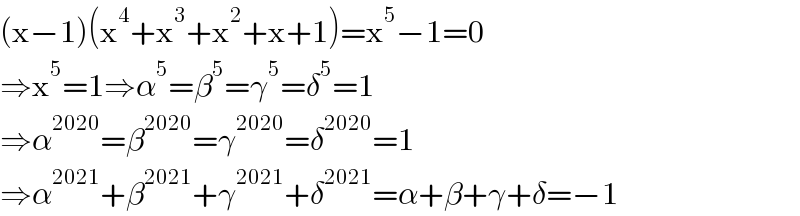
$$\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)=\mathrm{x}^{\mathrm{5}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{5}} =\mathrm{1}\Rightarrow\alpha^{\mathrm{5}} =\beta^{\mathrm{5}} =\gamma^{\mathrm{5}} =\delta^{\mathrm{5}} =\mathrm{1} \\ $$$$\Rightarrow\alpha^{\mathrm{2020}} =\beta^{\mathrm{2020}} =\gamma^{\mathrm{2020}} =\delta^{\mathrm{2020}} =\mathrm{1} \\ $$$$\Rightarrow\alpha^{\mathrm{2021}} +\beta^{\mathrm{2021}} +\gamma^{\mathrm{2021}} +\delta^{\mathrm{2021}} =\alpha+\beta+\gamma+\delta=−\mathrm{1} \\ $$
Answered by AntonCWX last updated on 18/Jan/25