Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 202436 by MATHEMATICSAM last updated on 26/Dec/23

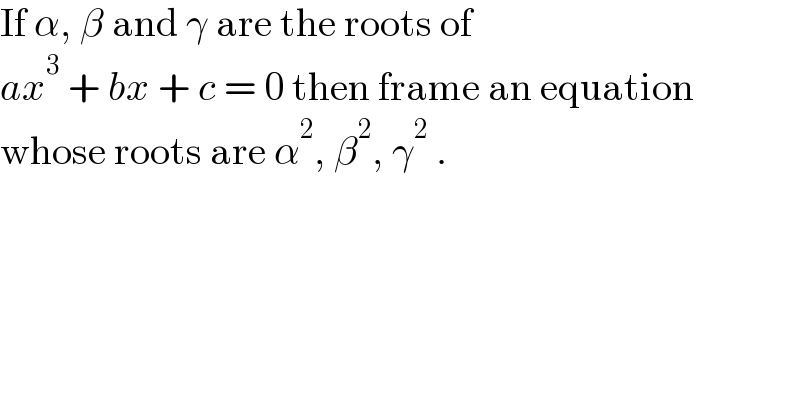
If α, β and γ are the roots of ax^3 + bx + c = 0 then frame an equation whose roots are α^2 , β^2 , γ^2 .

$$\mathrm{If}\:\alpha,\:\beta\:\mathrm{and}\:\gamma\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\: \\ $$$${ax}^{\mathrm{3}} \:+\:{bx}\:+\:{c}\:=\:\mathrm{0}\:\mathrm{then}\:\mathrm{frame}\:\mathrm{an}\:\mathrm{equation} \\ $$$$\mathrm{whose}\:\mathrm{roots}\:\mathrm{are}\:\alpha^{\mathrm{2}} ,\:\beta^{\mathrm{2}} ,\:\gamma^{\mathrm{2}} \:.\: \\ $$

Answered by aleks041103 last updated on 26/Dec/23

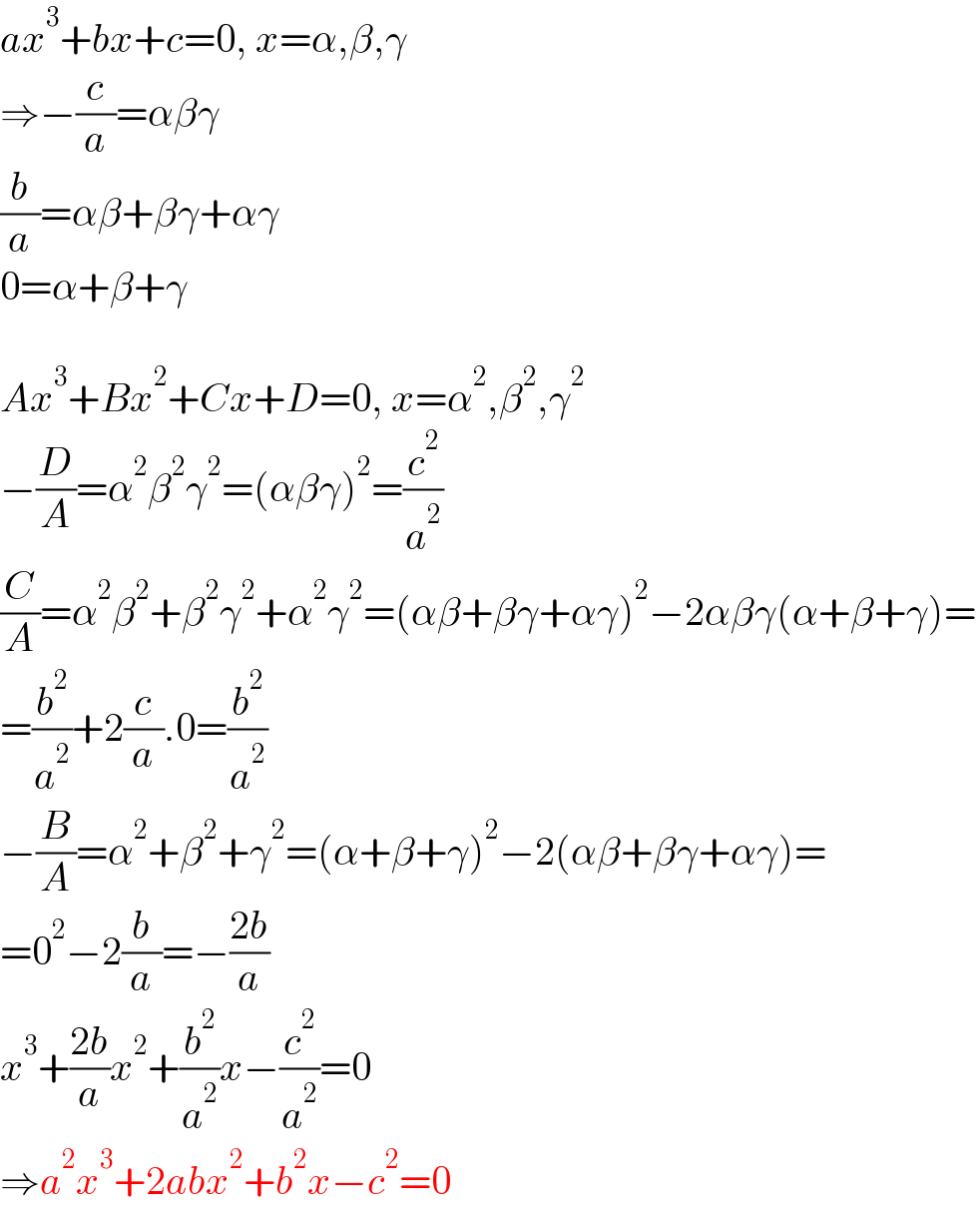
ax^3 +bx+c=0, x=α,β,γ ⇒−(c/a)=αβγ (b/a)=αβ+βγ+αγ 0=α+β+γ Ax^3 +Bx^2 +Cx+D=0, x=α^2 ,β^2 ,γ^2 −(D/A)=α^2 β^2 γ^2 =(αβγ)^2 =(c^2 /a^2 ) (C/A)=α^2 β^2 +β^2 γ^2 +α^2 γ^2 =(αβ+βγ+αγ)^2 −2αβγ(α+β+γ)= =(b^2 /a^2 )+2(c/a).0=(b^2 /a^2 ) −(B/A)=α^2 +β^2 +γ^2 =(α+β+γ)^2 −2(αβ+βγ+αγ)= =0^2 −2(b/a)=−((2b)/a) x^3 +((2b)/a)x^2 +(b^2 /a^2 )x−(c^2 /a^2 )=0 ⇒a^2 x^3 +2abx^2 +b^2 x−c^2 =0

$${ax}^{\mathrm{3}} +{bx}+{c}=\mathrm{0},\:{x}=\alpha,\beta,\gamma \\ $$$$\Rightarrow−\frac{{c}}{{a}}=\alpha\beta\gamma \\ $$$$\frac{{b}}{{a}}=\alpha\beta+\beta\gamma+\alpha\gamma \\ $$$$\mathrm{0}=\alpha+\beta+\gamma \\ $$$$ \\ $$$${Ax}^{\mathrm{3}} +{Bx}^{\mathrm{2}} +{Cx}+{D}=\mathrm{0},\:{x}=\alpha^{\mathrm{2}} ,\beta^{\mathrm{2}} ,\gamma^{\mathrm{2}} \\ $$$$−\frac{{D}}{{A}}=\alpha^{\mathrm{2}} \beta^{\mathrm{2}} \gamma^{\mathrm{2}} =\left(\alpha\beta\gamma\right)^{\mathrm{2}} =\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$$\frac{{C}}{{A}}=\alpha^{\mathrm{2}} \beta^{\mathrm{2}} +\beta^{\mathrm{2}} \gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} \gamma^{\mathrm{2}} =\left(\alpha\beta+\beta\gamma+\alpha\gamma\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta\gamma\left(\alpha+\beta+\gamma\right)= \\ $$$$=\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\mathrm{2}\frac{{c}}{{a}}.\mathrm{0}=\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$$−\frac{{B}}{{A}}=\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} =\left(\alpha+\beta+\gamma\right)^{\mathrm{2}} −\mathrm{2}\left(\alpha\beta+\beta\gamma+\alpha\gamma\right)= \\ $$$$=\mathrm{0}^{\mathrm{2}} −\mathrm{2}\frac{{b}}{{a}}=−\frac{\mathrm{2}{b}}{{a}} \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{2}{b}}{{a}}{x}^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{x}−\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {x}^{\mathrm{3}} +\mathrm{2}{abx}^{\mathrm{2}} +{b}^{\mathrm{2}} {x}−{c}^{\mathrm{2}} =\mathrm{0} \\ $$

Answered by Frix last updated on 27/Dec/23

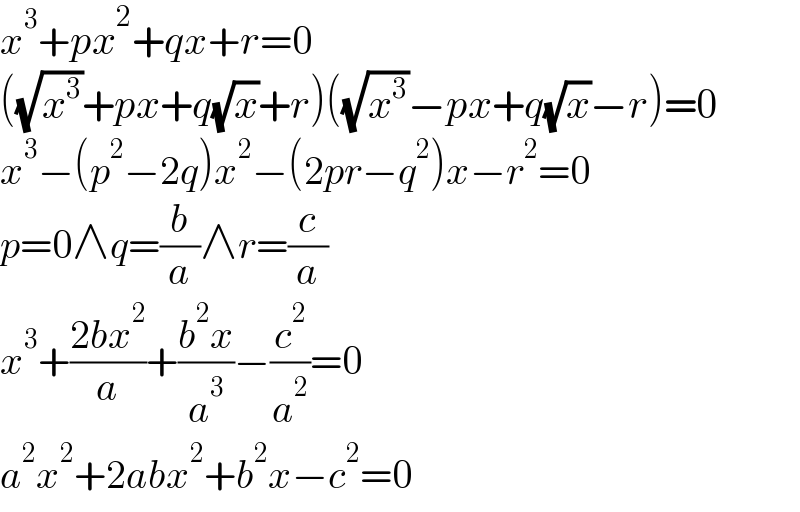
x^3 +px^2 +qx+r=0 ((√x^3 )+px+q(√x)+r)((√x^3 )−px+q(√x)−r)=0 x^3 −(p^2 −2q)x^2 −(2pr−q^2 )x−r^2 =0 p=0∧q=(b/a)∧r=(c/a) x^3 +((2bx^2 )/a)+((b^2 x)/a^3 )−(c^2 /a^2 )=0 a^2 x^2 +2abx^2 +b^2 x−c^2 =0

$${x}^{\mathrm{3}} +{px}^{\mathrm{2}} +{qx}+{r}=\mathrm{0} \\ $$$$\left(\sqrt{{x}^{\mathrm{3}} }+{px}+{q}\sqrt{{x}}+{r}\right)\left(\sqrt{{x}^{\mathrm{3}} }−{px}+{q}\sqrt{{x}}−{r}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\left({p}^{\mathrm{2}} −\mathrm{2}{q}\right){x}^{\mathrm{2}} −\left(\mathrm{2}{pr}−{q}^{\mathrm{2}} \right){x}−{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${p}=\mathrm{0}\wedge{q}=\frac{{b}}{{a}}\wedge{r}=\frac{{c}}{{a}} \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{2}{bx}^{\mathrm{2}} }{{a}}+\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{3}} }−\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mathrm{0} \\ $$$${a}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{abx}^{\mathrm{2}} +{b}^{\mathrm{2}} {x}−{c}^{\mathrm{2}} =\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com