Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 140973 by EnterUsername last updated on 14/May/21

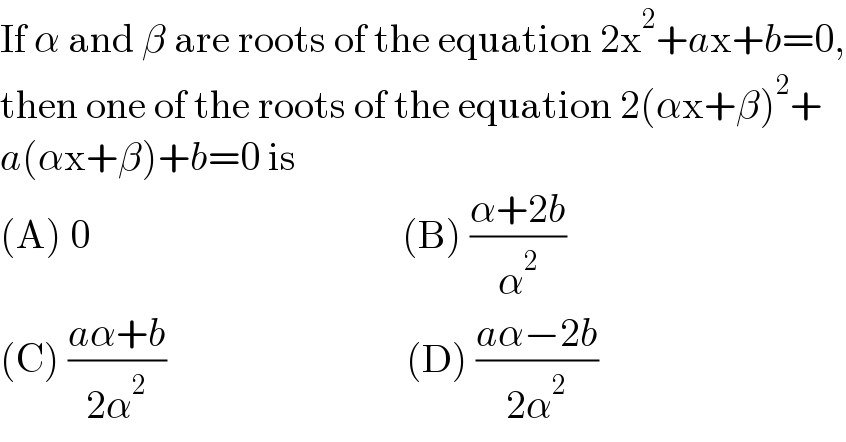
If α and β are roots of the equation 2x^2 +ax+b=0, then one of the roots of the equation 2(αx+β)^2 + a(αx+β)+b=0 is (A) 0 (B) ((α+2b)/α^2 ) (C) ((aα+b)/(2α^2 )) (D) ((aα−2b)/(2α^2 ))

$$\mathrm{If}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{2x}^{\mathrm{2}} +{a}\mathrm{x}+{b}=\mathrm{0}, \\ $$$$\mathrm{then}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{2}\left(\alpha\mathrm{x}+\beta\right)^{\mathrm{2}} + \\ $$$${a}\left(\alpha\mathrm{x}+\beta\right)+{b}=\mathrm{0}\:\mathrm{is} \\ $$$$\left(\mathrm{A}\right)\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\frac{\alpha+\mathrm{2}{b}}{\alpha^{\mathrm{2}} } \\ $$$$\left(\mathrm{C}\right)\:\frac{{a}\alpha+{b}}{\mathrm{2}\alpha^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\frac{{a}\alpha−\mathrm{2}{b}}{\mathrm{2}\alpha^{\mathrm{2}} } \\ $$

Answered by TheSupreme last updated on 15/May/21

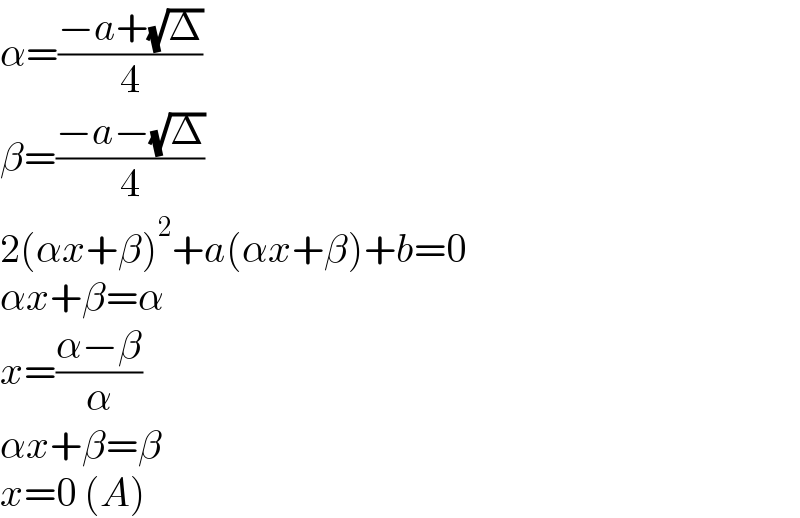
α=((−a+(√Δ))/4) β=((−a−(√Δ))/4) 2(αx+β)^2 +a(αx+β)+b=0 αx+β=α x=((α−β)/α) αx+β=β x=0 (A)

$$\alpha=\frac{−{a}+\sqrt{\Delta}}{\mathrm{4}} \\ $$$$\beta=\frac{−{a}−\sqrt{\Delta}}{\mathrm{4}} \\ $$$$\mathrm{2}\left(\alpha{x}+\beta\right)^{\mathrm{2}} +{a}\left(\alpha{x}+\beta\right)+{b}=\mathrm{0} \\ $$$$\alpha{x}+\beta=\alpha \\ $$$${x}=\frac{\alpha−\beta}{\alpha} \\ $$$$\alpha{x}+\beta=\beta \\ $$$${x}=\mathrm{0}\:\left({A}\right) \\ $$

Commented by EnterUsername last updated on 19/May/21

Thanks so much

$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com