
Question Number 207021 by efronzo1 last updated on 03/May/24
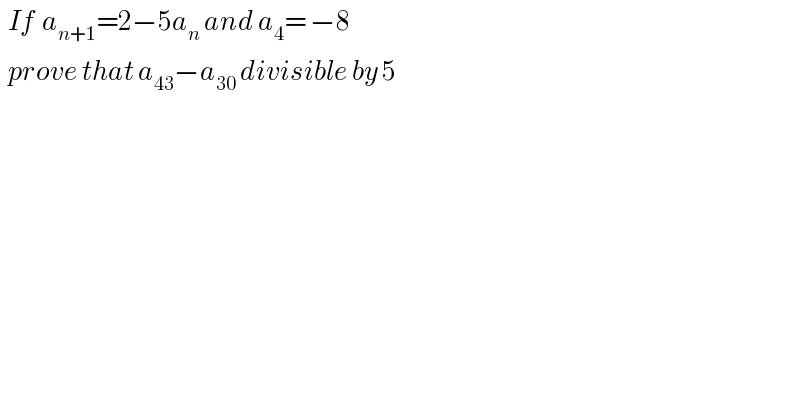
$$\:\:{If}\:\:{a}_{{n}+\mathrm{1}} =\mathrm{2}−\mathrm{5}{a}_{{n}} \:{and}\:{a}_{\mathrm{4}} =\:−\mathrm{8} \\ $$$$\:\:{prove}\:{that}\:{a}_{\mathrm{43}} −{a}_{\mathrm{30}} \:{divisible}\:{by}\:\mathrm{5} \\ $$
Commented by mr W last updated on 04/May/24
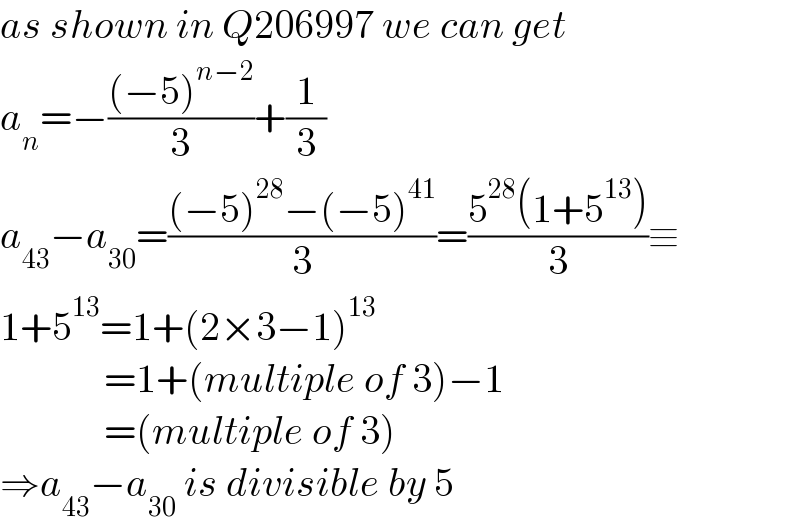
$${as}\:{shown}\:{in}\:{Q}\mathrm{206997}\:{we}\:{can}\:{get} \\ $$$${a}_{{n}} =−\frac{\left(−\mathrm{5}\right)^{{n}−\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${a}_{\mathrm{43}} −{a}_{\mathrm{30}} =\frac{\left(−\mathrm{5}\right)^{\mathrm{28}} −\left(−\mathrm{5}\right)^{\mathrm{41}} }{\mathrm{3}}=\frac{\mathrm{5}^{\mathrm{28}} \left(\mathrm{1}+\mathrm{5}^{\mathrm{13}} \right)}{\mathrm{3}}\equiv \\ $$$$\mathrm{1}+\mathrm{5}^{\mathrm{13}} =\mathrm{1}+\left(\mathrm{2}×\mathrm{3}−\mathrm{1}\right)^{\mathrm{13}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\left({multiple}\:{of}\:\mathrm{3}\right)−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({multiple}\:{of}\:\mathrm{3}\right) \\ $$$$\Rightarrow{a}_{\mathrm{43}} −{a}_{\mathrm{30}} \:{is}\:{divisible}\:{by}\:\mathrm{5} \\ $$
Answered by Berbere last updated on 04/May/24
![a_(n+1) ≡2[5];∀n≥4∴ a_(n+1) =2−5.a_n ∵ a_(43) ≡2[5];a_(30) ≡2[5]⇒a_(43) −a_(30) ≡0[5]](Q207051.png)
$${a}_{{n}+\mathrm{1}} \equiv\mathrm{2}\left[\mathrm{5}\right];\forall{n}\geqslant\mathrm{4}\therefore\:{a}_{{n}+\mathrm{1}} =\mathrm{2}−\mathrm{5}.{a}_{{n}} \because \\ $$$${a}_{\mathrm{43}} \equiv\mathrm{2}\left[\mathrm{5}\right];{a}_{\mathrm{30}} \equiv\mathrm{2}\left[\mathrm{5}\right]\Rightarrow{a}_{\mathrm{43}} −{a}_{\mathrm{30}} \equiv\mathrm{0}\left[\mathrm{5}\right] \\ $$
