
Question Number 194779 by sniper237 last updated on 15/Jul/23
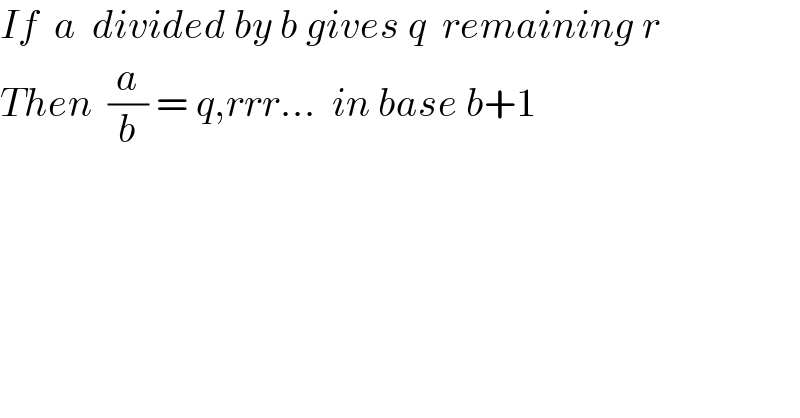
$${If}\:\:{a}\:\:{divided}\:{by}\:{b}\:{gives}\:{q}\:\:{remaining}\:{r} \\ $$$${Then}\:\:\frac{{a}}{{b}}\:=\:{q},{rrr}...\:\:{in}\:{base}\:{b}+\mathrm{1} \\ $$
Commented by Frix last updated on 15/Jul/23
No problem ��
Commented by Frix last updated on 15/Jul/23
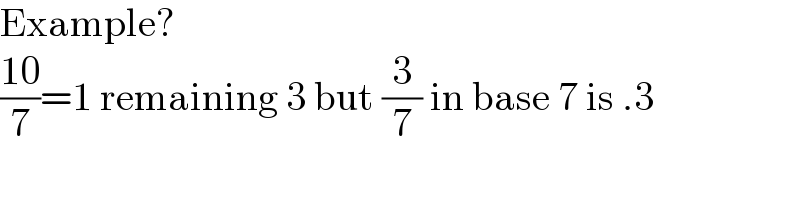
$$\mathrm{Example}? \\ $$$$\frac{\mathrm{10}}{\mathrm{7}}=\mathrm{1}\:\mathrm{remaining}\:\mathrm{3}\:\mathrm{but}\:\frac{\mathrm{3}}{\mathrm{7}}\:\mathrm{in}\:\mathrm{base}\:\mathrm{7}\:\mathrm{is}\:.\mathrm{3} \\ $$
Commented by Frix last updated on 15/Jul/23
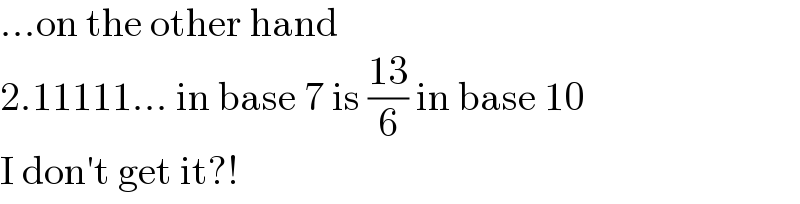
$$...\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hand} \\ $$$$\mathrm{2}.\mathrm{11111}...\:\mathrm{in}\:\mathrm{base}\:\mathrm{7}\:\mathrm{is}\:\frac{\mathrm{13}}{\mathrm{6}}\:\mathrm{in}\:\mathrm{base}\:\mathrm{10} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}\:\mathrm{it}?! \\ $$
Commented by sniper237 last updated on 15/Jul/23

$${Sorry}\:{for}\:{all} \\ $$
Answered by deleteduser1 last updated on 15/Jul/23
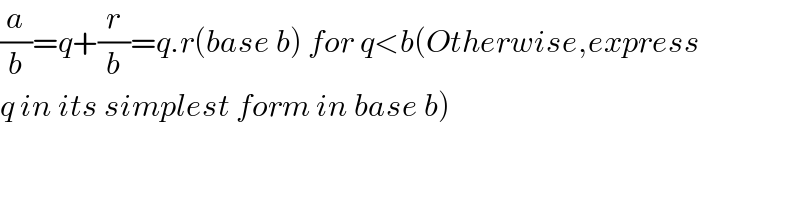
$$\frac{{a}}{{b}}={q}+\frac{{r}}{{b}}={q}.{r}\left({base}\:{b}\right)\:{for}\:{q}<{b}\left({Otherwise},{express}\right. \\ $$$$\left.{q}\:{in}\:{its}\:{simplest}\:{form}\:{in}\:{base}\:{b}\right) \\ $$
