
Question Number 54970 by Tip Top last updated on 15/Feb/19
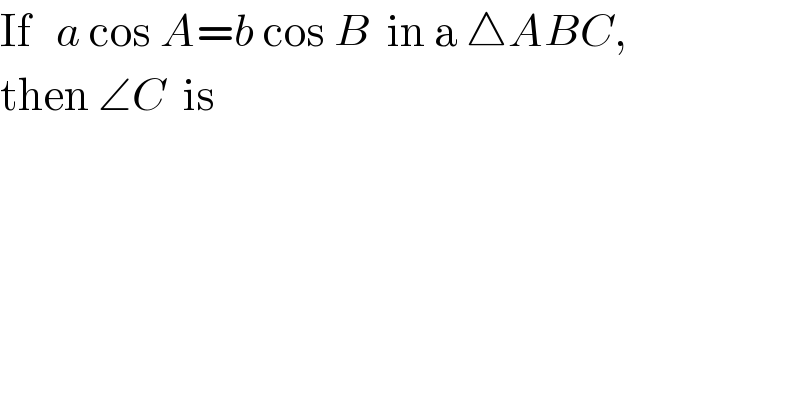
$$\mathrm{If}\:\:\:{a}\:\mathrm{cos}\:{A}={b}\:\mathrm{cos}\:{B}\:\:\mathrm{in}\:\mathrm{a}\:\bigtriangleup{ABC},\: \\ $$$$\mathrm{then}\:\angle{C}\:\:\mathrm{is} \\ $$
Answered by $@ty@m last updated on 15/Feb/19
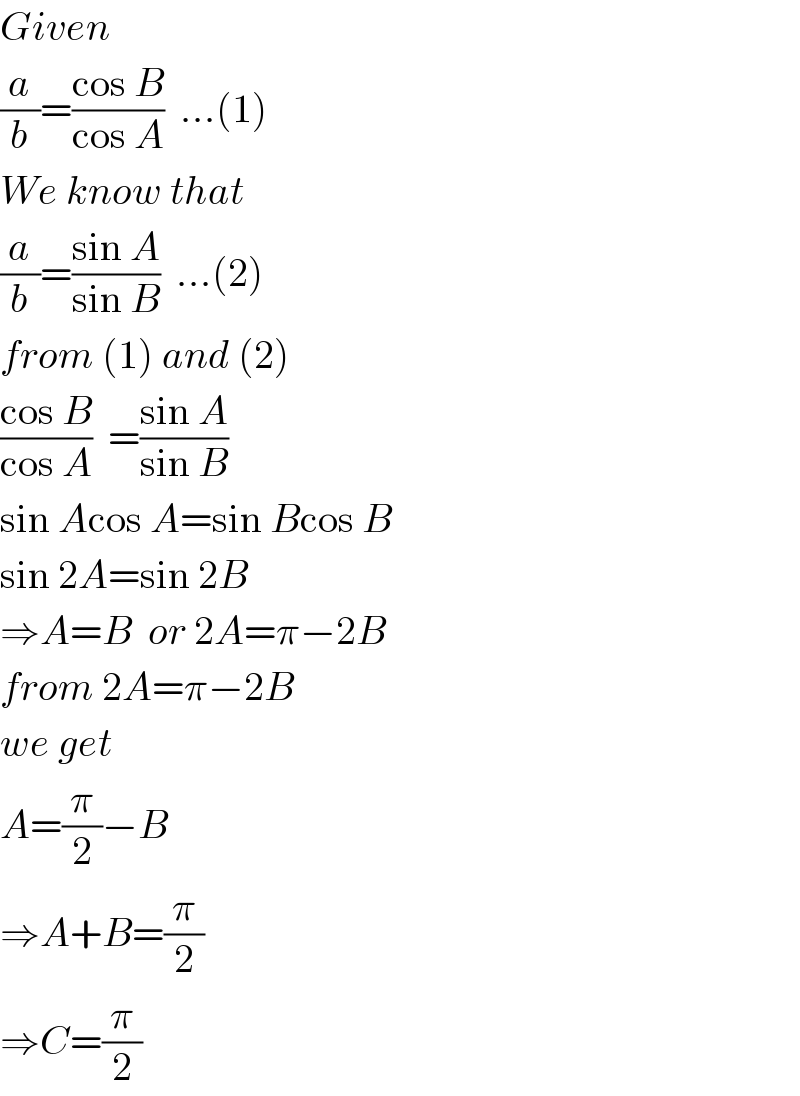
$${Given} \\ $$$$\frac{{a}}{{b}}=\frac{\mathrm{cos}\:{B}}{\mathrm{cos}\:{A}}\:\:...\left(\mathrm{1}\right) \\ $$$${We}\:{know}\:{that} \\ $$$$\frac{{a}}{{b}}=\frac{\mathrm{sin}\:{A}}{\mathrm{sin}\:{B}}\:\:...\left(\mathrm{2}\right) \\ $$$${from}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$$\frac{\mathrm{cos}\:{B}}{\mathrm{cos}\:{A}}\:\:=\frac{\mathrm{sin}\:{A}}{\mathrm{sin}\:{B}} \\ $$$$\mathrm{sin}\:{A}\mathrm{cos}\:{A}=\mathrm{sin}\:{B}\mathrm{cos}\:{B} \\ $$$$\mathrm{sin}\:\mathrm{2}{A}=\mathrm{sin}\:\mathrm{2}{B} \\ $$$$\Rightarrow{A}={B}\:\:{or}\:\mathrm{2}{A}=\pi−\mathrm{2}{B} \\ $$$${from}\:\mathrm{2}{A}=\pi−\mathrm{2}{B} \\ $$$${we}\:{get} \\ $$$${A}=\frac{\pi}{\mathrm{2}}−{B} \\ $$$$\Rightarrow{A}+{B}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{C}=\frac{\pi}{\mathrm{2}} \\ $$
