Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 205423 by hardmath last updated on 20/Mar/24

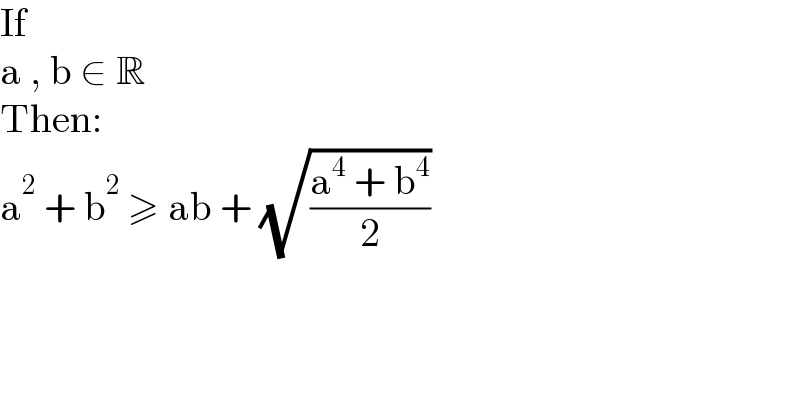
If a , b ∈ R Then: a^2 + b^2 ≥ ab + (√((a^4 + b^4 )/2))

$$\mathrm{If} \\ $$$$\mathrm{a}\:,\:\mathrm{b}\:\in\:\mathbb{R} \\ $$$$\mathrm{Then}: \\ $$$$\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} \:\geqslant\:\mathrm{ab}\:+\:\sqrt{\frac{\mathrm{a}^{\mathrm{4}} \:+\:\mathrm{b}^{\mathrm{4}} }{\mathrm{2}}} \\ $$

Answered by Berbere last updated on 21/Mar/24

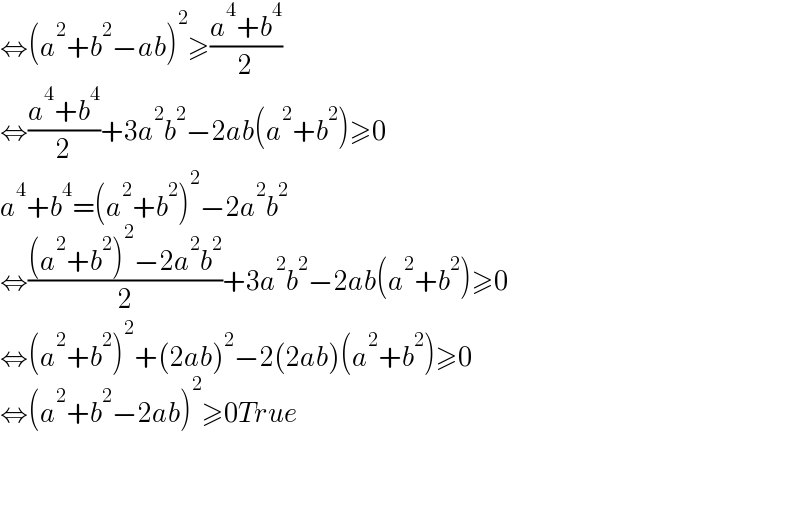
⇔(a^2 +b^2 −ab)^2 ≥((a^4 +b^4 )/2) ⇔((a^4 +b^4 )/2)+3a^2 b^2 −2ab(a^2 +b^2 )≥0 a^4 +b^4 =(a^2 +b^2 )^2 −2a^2 b^2 ⇔(((a^2 +b^2 )^2 −2a^2 b^2 )/2)+3a^2 b^2 −2ab(a^2 +b^2 )≥0 ⇔(a^2 +b^2 )^2 +(2ab)^2 −2(2ab)(a^2 +b^2 )≥0 ⇔(a^2 +b^2 −2ab)^2 ≥0True

$$\Leftrightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)^{\mathrm{2}} \geqslant\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }{\mathrm{2}} \\ $$$$\Leftrightarrow\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }{\mathrm{2}}+\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}{ab}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\geqslant\mathrm{0} \\ $$$${a}^{\mathrm{4}} +{b}^{\mathrm{4}} =\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Leftrightarrow\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}{ab}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\geqslant\mathrm{0} \\ $$$$\Leftrightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{2}{ab}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}{ab}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\geqslant\mathrm{0} \\ $$$$\Leftrightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\right)^{\mathrm{2}} \geqslant\mathrm{0}{True} \\ $$$$ \\ $$$$ \\ $$

Commented by Skabetix last updated on 22/Mar/24

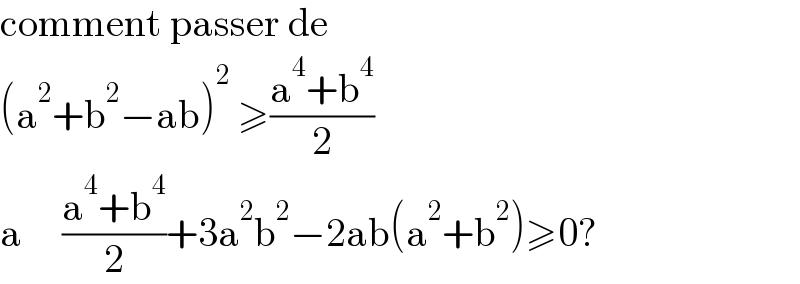
comment passer de (a^2 +b^2 −ab)^2 ≥((a^4 +b^4 )/2) a ((a^4 +b^4 )/2)+3a^2 b^2 −2ab(a^2 +b^2 )≥0?

$$\mathrm{comment}\:\mathrm{passer}\:\mathrm{de}\: \\ $$$$\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{ab}\right)^{\mathrm{2}} \:\geqslant\frac{\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} }{\mathrm{2}} \\ $$$$\mathrm{a}\:\:\:\:\:\frac{\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} }{\mathrm{2}}+\mathrm{3a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} −\mathrm{2ab}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)\geqslant\mathrm{0}? \\ $$

Commented by Berbere last updated on 24/Mar/24

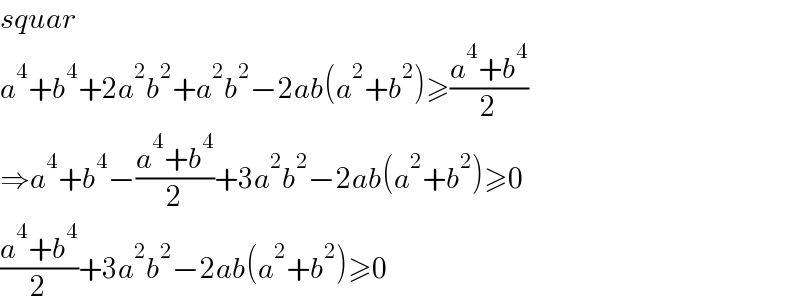
squar a^4 +b^4 +2a^2 b^2 +a^2 b^2 −2ab(a^2 +b^2 )≥((a^4 +b^4 )/2) ⇒a^4 +b^4 −((a^4 +b^4 )/2)+3a^2 b^2 −2ab(a^2 +b^2 )≥0 ((a^4 +b^4 )/2)+3a^2 b^2 −2ab(a^2 +b^2 )≥0

$${squar} \\ $$$${a}^{\mathrm{4}} +{b}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}{ab}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\geqslant\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{4}} +{b}^{\mathrm{4}} −\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }{\mathrm{2}}+\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}{ab}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\geqslant\mathrm{0} \\ $$$$\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }{\mathrm{2}}+\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}{ab}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\geqslant\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com