Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 193180 by BaliramKumar last updated on 06/Jun/23

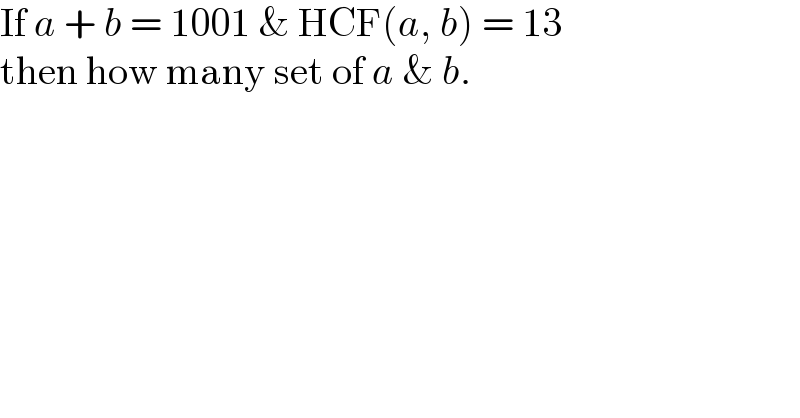
If a + b = 1001 & HCF(a, b) = 13 then how many set of a & b.

$$\mathrm{If}\:{a}\:+\:{b}\:=\:\mathrm{1001}\:\&\:\mathrm{HCF}\left({a},\:{b}\right)\:=\:\mathrm{13}\: \\ $$$$\mathrm{then}\:\mathrm{how}\:\mathrm{many}\:\mathrm{set}\:\mathrm{of}\:{a}\:\&\:{b}. \\ $$

Answered by Subhi last updated on 06/Jun/23

a = 13k b = 13m a+b = 1001 = 13(k+m) k+m = 77 there are 78 pairs (77,0),(76,1).............(1,76),(0,77) there are restricrions when m and k are divisible by 11 or 7 m = 7l k = 7n k+m = 77 = 7(l+n) l+n = 11 (l,n) = (10,1),(9,2),(8,3),(7,4),(6,5)........(1,10) 10 pairs are excluded (ii) m = 11g k = 11h k+m = 77 = 11(g+h) g+h = 7 (g,h) = (6,1),(5,2),(4,3).....(1,6) 6 pairs are excluded 78−6−10 = 62

$${a}\:=\:\mathrm{13}{k} \\ $$$${b}\:=\:\mathrm{13}{m} \\ $$$${a}+{b}\:=\:\mathrm{1001}\:=\:\mathrm{13}\left({k}+{m}\right) \\ $$$${k}+{m}\:=\:\mathrm{77} \\ $$$${there}\:{are}\:\mathrm{78}\:{pairs} \\ $$$$\left(\mathrm{77},\mathrm{0}\right),\left(\mathrm{76},\mathrm{1}\right).............\left(\mathrm{1},\mathrm{76}\right),\left(\mathrm{0},\mathrm{77}\right) \\ $$$${there}\:{are}\:{restricrions}\:{when}\:{m}\:{and}\:{k}\:{are}\:{divisible}\:{by}\:\mathrm{11}\:{or}\:\mathrm{7} \\ $$$${m}\:=\:\mathrm{7}{l} \\ $$$${k}\:=\:\mathrm{7}{n} \\ $$$${k}+{m}\:=\:\mathrm{77}\:=\:\mathrm{7}\left({l}+{n}\right) \\ $$$${l}+{n}\:=\:\mathrm{11} \\ $$$$\left({l},{n}\right)\:=\:\left(\mathrm{10},\mathrm{1}\right),\left(\mathrm{9},\mathrm{2}\right),\left(\mathrm{8},\mathrm{3}\right),\left(\mathrm{7},\mathrm{4}\right),\left(\mathrm{6},\mathrm{5}\right)........\left(\mathrm{1},\mathrm{10}\right) \\ $$$$\mathrm{10}\:{pairs}\:\:{are}\:{excluded} \\ $$$$\left({ii}\right)\:{m}\:=\:\mathrm{11}{g} \\ $$$${k}\:=\:\mathrm{11}{h} \\ $$$${k}+{m}\:=\:\mathrm{77}\:=\:\mathrm{11}\left({g}+{h}\right) \\ $$$${g}+{h}\:=\:\mathrm{7} \\ $$$$\left({g},{h}\right)\:=\:\left(\mathrm{6},\mathrm{1}\right),\left(\mathrm{5},\mathrm{2}\right),\left(\mathrm{4},\mathrm{3}\right).....\left(\mathrm{1},\mathrm{6}\right) \\ $$$$\mathrm{6}\:{pairs}\:{are}\:{excluded} \\ $$$$\mathrm{78}−\mathrm{6}−\mathrm{10}\:=\:\mathrm{62} \\ $$

Commented by MM42 last updated on 06/Jun/23

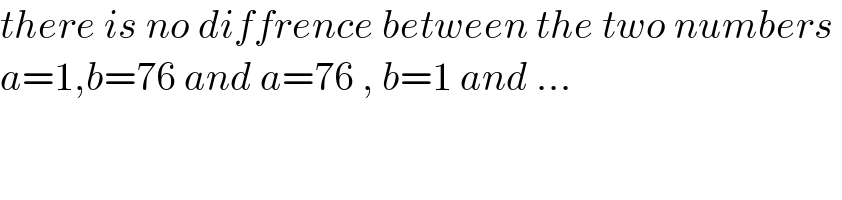
there is no diffrence between the two numbers a=1,b=76 and a=76 , b=1 and ...

$${there}\:{is}\:{no}\:{diffrence}\:{between}\:{the}\:{two}\:{numbers}\: \\ $$$${a}=\mathrm{1},{b}=\mathrm{76}\:{and}\:{a}=\mathrm{76}\:,\:{b}=\mathrm{1}\:{and}\:... \\ $$

Commented by Subhi last updated on 06/Jun/23

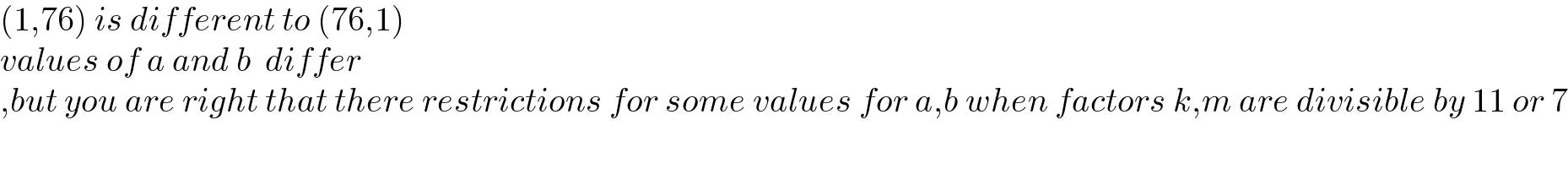
(1,76) is different to (76,1) values of a and b differ ,but you are right that there restrictions for some values for a,b when factors k,m are divisible by 11 or 7

$$\left(\mathrm{1},\mathrm{76}\right)\:{is}\:{different}\:{to}\:\left(\mathrm{76},\mathrm{1}\right) \\ $$$${values}\:{of}\:{a}\:{and}\:{b}\:\:{differ} \\ $$$$,{but}\:{you}\:{are}\:{right}\:{that}\:{there}\:{restrictions}\:{for}\:{some}\:{values}\:{for}\:{a},{b}\:{when}\:{factors}\:{k},{m}\:{are}\:{divisible}\:{by}\:\mathrm{11}\:{or}\:\mathrm{7} \\ $$

Commented by Subhi last updated on 06/Jun/23

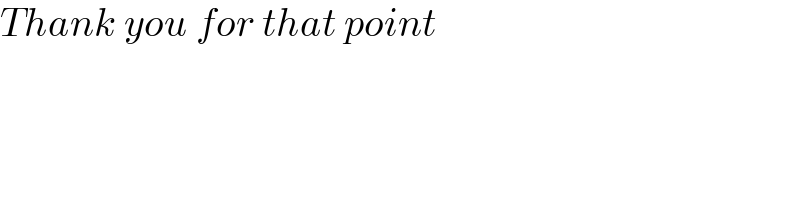
Thank you for that point

$${Thank}\:{you}\:{for}\:{that}\:{point} \\ $$

Commented by BaliramKumar last updated on 07/Jun/23

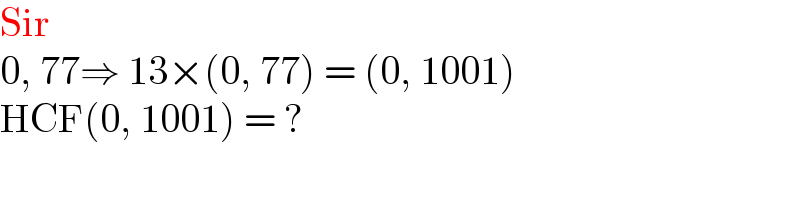
Sir 0, 77⇒ 13×(0, 77) = (0, 1001) HCF(0, 1001) = ?

$$\mathrm{Sir} \\ $$$$\mathrm{0},\:\mathrm{77}\Rightarrow\:\mathrm{13}×\left(\mathrm{0},\:\mathrm{77}\right)\:=\:\left(\mathrm{0},\:\mathrm{1001}\right) \\ $$$$\mathrm{HCF}\left(\mathrm{0},\:\mathrm{1001}\right)\:=\:? \\ $$

Commented by MM42 last updated on 07/Jun/23

you are right

$${you}\:{are}\:{right} \\ $$

Answered by MM42 last updated on 07/Jun/23

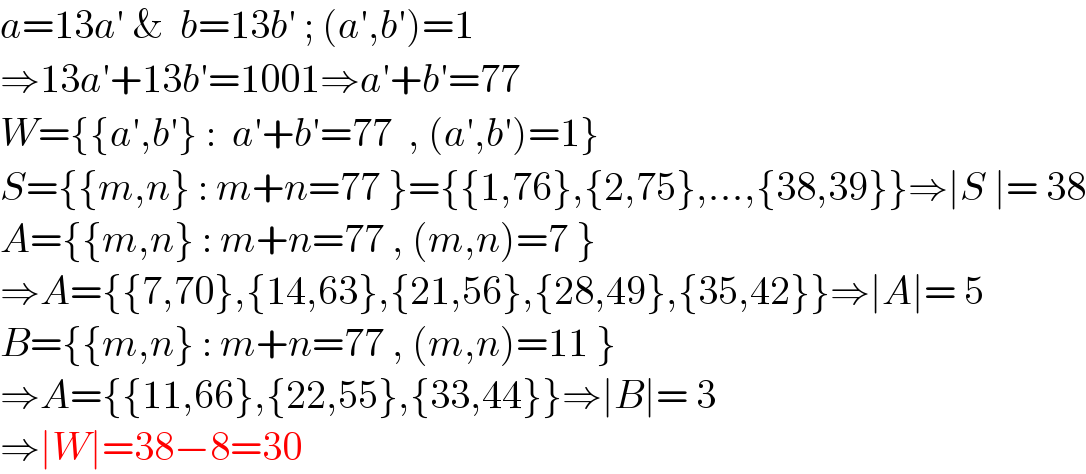
a=13a′ & b=13b′ ; (a′,b′)=1 ⇒13a′+13b′=1001⇒a′+b′=77 W={{a′,b′} : a′+b′=77 , (a′,b′)=1} S={{m,n} : m+n=77 }={{1,76},{2,75},...,{38,39}}⇒∣S ∣= 38 A={{m,n} : m+n=77 , (m,n)=7 } ⇒A={{7,70},{14,63},{21,56},{28,49},{35,42}}⇒∣A∣= 5 B={{m,n} : m+n=77 , (m,n)=11 } ⇒A={{11,66},{22,55},{33,44}}⇒∣B∣= 3 ⇒∣W∣=38−8=30

$${a}=\mathrm{13}{a}'\:\&\:\:{b}=\mathrm{13}{b}'\:;\:\left({a}',{b}'\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{13}{a}'+\mathrm{13}{b}'=\mathrm{1001}\Rightarrow{a}'+{b}'=\mathrm{77} \\ $$$${W}=\left\{\left\{{a}',{b}'\right\}\::\:\:{a}'+{b}'=\mathrm{77}\:\:,\:\left({a}',{b}'\right)=\mathrm{1}\right\} \\ $$$${S}=\left\{\left\{{m},{n}\right\}\::\:{m}+{n}=\mathrm{77}\:\right\}=\left\{\left\{\mathrm{1},\mathrm{76}\right\},\left\{\mathrm{2},\mathrm{75}\right\},...,\left\{\mathrm{38},\mathrm{39}\right\}\right\}\Rightarrow\mid{S}\:\mid=\:\mathrm{38} \\ $$$${A}=\left\{\left\{{m},{n}\right\}\::\:{m}+{n}=\mathrm{77}\:,\:\left({m},{n}\right)=\mathrm{7}\:\right\} \\ $$$$\Rightarrow{A}=\left\{\left\{\mathrm{7},\mathrm{70}\right\},\left\{\mathrm{14},\mathrm{63}\right\},\left\{\mathrm{21},\mathrm{56}\right\},\left\{\mathrm{28},\mathrm{49}\right\},\left\{\mathrm{35},\mathrm{42}\right\}\right\}\Rightarrow\mid{A}\mid=\:\mathrm{5} \\ $$$${B}=\left\{\left\{{m},{n}\right\}\::\:{m}+{n}=\mathrm{77}\:,\:\left({m},{n}\right)=\mathrm{11}\:\right\} \\ $$$$\Rightarrow{A}=\left\{\left\{\mathrm{11},\mathrm{66}\right\},\left\{\mathrm{22},\mathrm{55}\right\},\left\{\mathrm{33},\mathrm{44}\right\}\right\}\Rightarrow\mid{B}\mid=\:\mathrm{3} \\ $$$$\Rightarrow\mid{W}\mid=\mathrm{38}−\mathrm{8}=\mathrm{30} \\ $$

Answered by BaliramKumar last updated on 18/Nov/23

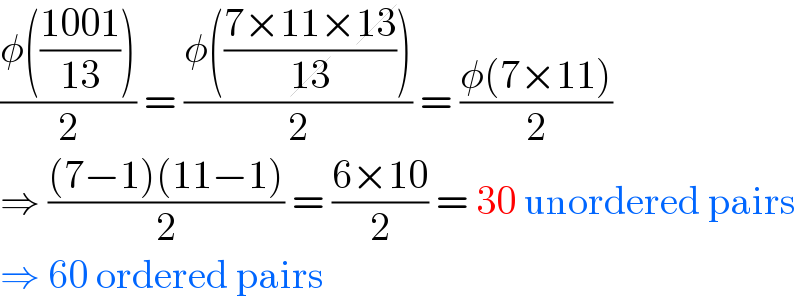
((φ(((1001)/(13))))/2) = ((φ(((7×11×13)/(13))))/2) = ((φ(7×11))/2) ⇒ (((7−1)(11−1))/2) = ((6×10)/2) = 30 unordered pairs ⇒ 60 ordered pairs

$$\frac{\phi\left(\frac{\mathrm{1001}}{\mathrm{13}}\right)}{\mathrm{2}}\:=\:\frac{\phi\left(\frac{\mathrm{7}×\mathrm{11}×\cancel{\mathrm{13}}}{\cancel{\mathrm{13}}}\right)}{\mathrm{2}}\:=\:\frac{\phi\left(\mathrm{7}×\mathrm{11}\right)}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\left(\mathrm{7}−\mathrm{1}\right)\left(\mathrm{11}−\mathrm{1}\right)}{\mathrm{2}}\:=\:\frac{\mathrm{6}×\mathrm{10}}{\mathrm{2}}\:=\:\mathrm{30}\:\mathrm{unordered}\:\mathrm{pairs} \\ $$$$\Rightarrow\:\mathrm{60}\:\mathrm{ordered}\:\mathrm{pairs} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com