
Question Number 202044 by hardmath last updated on 19/Dec/23

$$\mathrm{If} \\ $$$$\mathrm{a}\:=\:\mathrm{9999999998000000001} \\ $$$$\mathrm{Find} \\ $$$$\mathrm{A}\:=\:\sqrt[{\mathrm{9}}]{\sqrt{\mathrm{a}}\:+\:\mathrm{1}}\:\:\:\rightarrow\:\:\:\mathrm{A}\:=\:? \\ $$
Commented by mr W last updated on 19/Dec/23
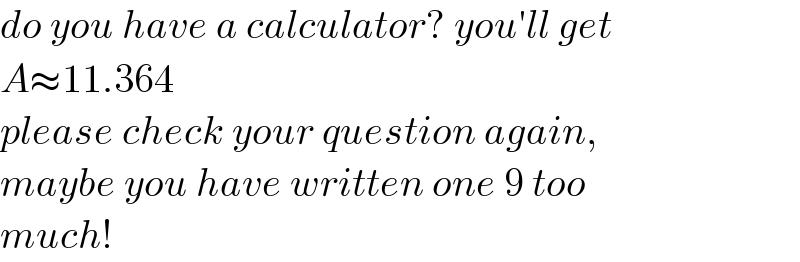
$${do}\:{you}\:{have}\:{a}\:{calculator}?\:{you}'{ll}\:{get} \\ $$$${A}\approx\mathrm{11}.\mathrm{364} \\ $$$${please}\:{check}\:{your}\:{question}\:{again}, \\ $$$${maybe}\:{you}\:{have}\:{written}\:{one}\:\mathrm{9}\:{too}\: \\ $$$${much}! \\ $$
Answered by esmaeil last updated on 19/Dec/23
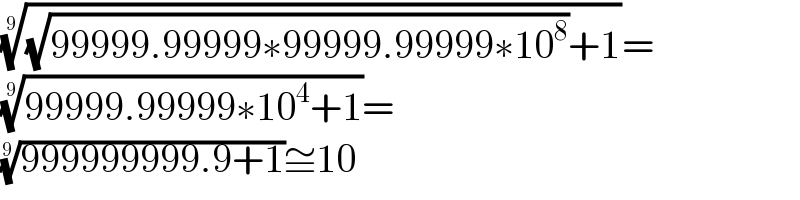
$$\sqrt[{\mathrm{9}}]{\sqrt{\mathrm{99999}.\mathrm{99999}\ast\mathrm{99999}.\mathrm{99999}\ast\mathrm{10}^{\mathrm{8}} }+\mathrm{1}}= \\ $$$$\sqrt[{\mathrm{9}}]{\mathrm{99999}.\mathrm{99999}\ast\mathrm{10}^{\mathrm{4}} +\mathrm{1}}= \\ $$$$\sqrt[{\mathrm{9}}]{\mathrm{999999999}.\mathrm{9}+\mathrm{1}}\cong\mathrm{10} \\ $$
Answered by mr W last updated on 20/Dec/23
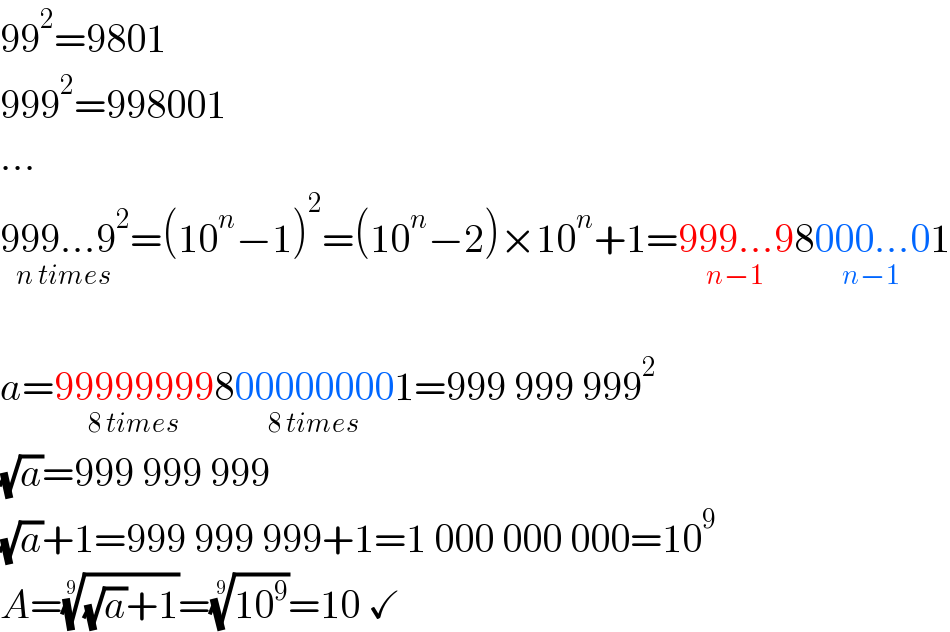
$$\mathrm{99}^{\mathrm{2}} =\mathrm{9801} \\ $$$$\mathrm{999}^{\mathrm{2}} =\mathrm{998001} \\ $$$$... \\ $$$$\underset{{n}\:{times}} {\mathrm{999}...\mathrm{9}^{\mathrm{2}} }=\left(\mathrm{10}^{{n}} −\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{10}^{{n}} −\mathrm{2}\right)×\mathrm{10}^{{n}} +\mathrm{1}=\underset{{n}−\mathrm{1}} {\mathrm{999}...\mathrm{9}8}\underset{{n}−\mathrm{1}} {\mathrm{000}...\mathrm{0}1} \\ $$$$ \\ $$$${a}=\underset{\mathrm{8}\:{times}} {\mathrm{99999999}8}\underset{\mathrm{8}\:{times}} {\mathrm{00000000}1}=\mathrm{999}\:\mathrm{999}\:\mathrm{999}^{\mathrm{2}} \\ $$$$\sqrt{{a}}=\mathrm{999}\:\mathrm{999}\:\mathrm{999} \\ $$$$\sqrt{{a}}+\mathrm{1}=\mathrm{999}\:\mathrm{999}\:\mathrm{999}+\mathrm{1}=\mathrm{1}\:\mathrm{000}\:\mathrm{000}\:\mathrm{000}=\mathrm{10}^{\mathrm{9}} \\ $$$${A}=\sqrt[{\mathrm{9}}]{\sqrt{{a}}+\mathrm{1}}=\sqrt[{\mathrm{9}}]{\mathrm{10}^{\mathrm{9}} }=\mathrm{10}\:\checkmark \\ $$
Commented by hardmath last updated on 20/Dec/23
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thankyou} \\ $$
