
Question Number 201237 by mnjuly1970 last updated on 02/Dec/23
![If , a ∣ 5b^( 2) −10b +1 ⇒ [ a , 5b ]_(lcm) = ?](Q201237.png)
$$ \\ $$$$\:\:\:\:{If}\:\:,\:\:\:{a}\:\mid\:\mathrm{5}{b}^{\:\mathrm{2}} −\mathrm{10}{b}\:+\mathrm{1}\: \\ $$$$\:\:\:\:\:\Rightarrow\:\:\:\left[\:{a}\:\:,\:\mathrm{5}{b}\:\right]_{\mathrm{lc}{m}} \:=\:\:?\: \\ $$$$ \\ $$$$ \\ $$
Commented by deleteduser1 last updated on 02/Dec/23

$${lcd}? \\ $$
Commented by Rasheed.Sindhi last updated on 02/Dec/23

$$\mathrm{5}{ab}? \\ $$
Commented by mnjuly1970 last updated on 02/Dec/23

$${lcm}\:... \\ $$
Answered by witcher3 last updated on 02/Dec/23
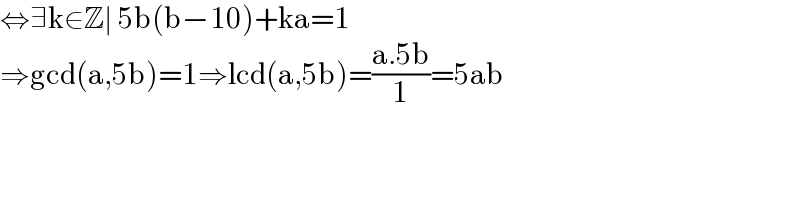
$$\Leftrightarrow\exists\mathrm{k}\in\mathbb{Z}\mid\:\mathrm{5b}\left(\mathrm{b}−\mathrm{10}\right)+\mathrm{ka}=\mathrm{1}\: \\ $$$$\Rightarrow\mathrm{gcd}\left(\mathrm{a},\mathrm{5b}\right)=\mathrm{1}\Rightarrow\mathrm{lcd}\left(\mathrm{a},\mathrm{5b}\right)=\frac{\mathrm{a}.\mathrm{5b}}{\mathrm{1}}=\mathrm{5ab} \\ $$
Commented by deleteduser1 last updated on 02/Dec/23

$${lcm}\:{or}\:{lcd}? \\ $$
Commented by witcher3 last updated on 02/Dec/23
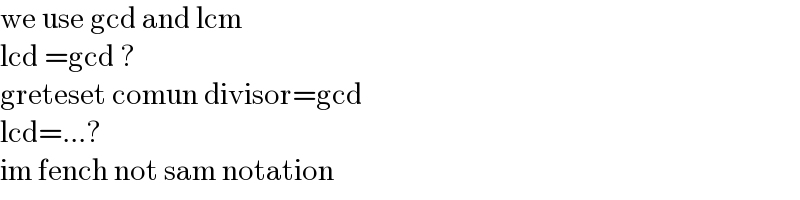
$$\mathrm{we}\:\mathrm{use}\:\mathrm{gcd}\:\mathrm{and}\:\mathrm{lcm}\: \\ $$$$\mathrm{lcd}\:=\mathrm{gcd}\:? \\ $$$$\mathrm{greteset}\:\mathrm{comun}\:\mathrm{divisor}=\mathrm{gcd} \\ $$$$\mathrm{lcd}=...? \\ $$$$\mathrm{im}\:\mathrm{fench}\:\mathrm{not}\:\mathrm{sam}\:\mathrm{notation} \\ $$
