Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 203941 by Panav last updated on 02/Feb/24

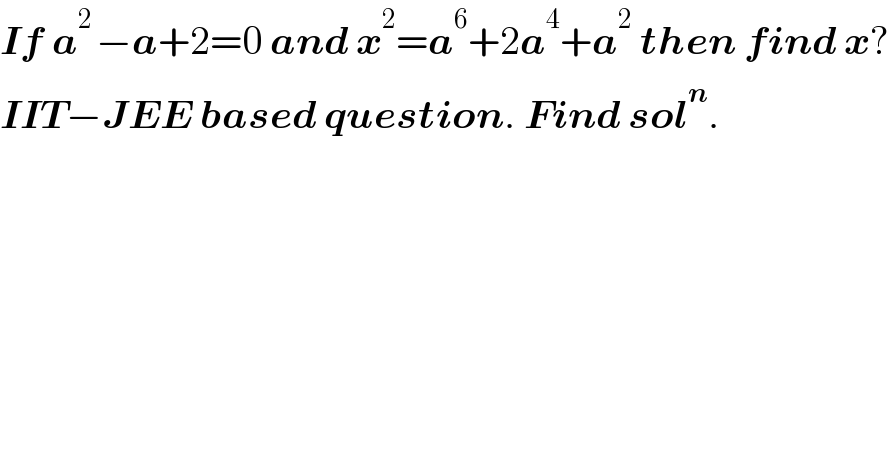
If a^(2 ) −a+2=0 and x^2 =a^6 +2a^4 +a^2 then find x? IIT−JEE based question. Find sol^n .

$$\boldsymbol{{If}}\:\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\:\boldsymbol{{and}}\:\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{a}}^{\mathrm{6}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{4}} +\boldsymbol{{a}}^{\mathrm{2}} \:\boldsymbol{{then}}\:\boldsymbol{{find}}\:\boldsymbol{{x}}? \\ $$$$\boldsymbol{{IIT}}−\boldsymbol{{JEE}}\:\boldsymbol{{based}}\:\boldsymbol{{question}}.\:\boldsymbol{{Find}}\:\boldsymbol{{sol}}^{\boldsymbol{{n}}} . \\ $$

Answered by Rasheed.Sindhi last updated on 02/Feb/24

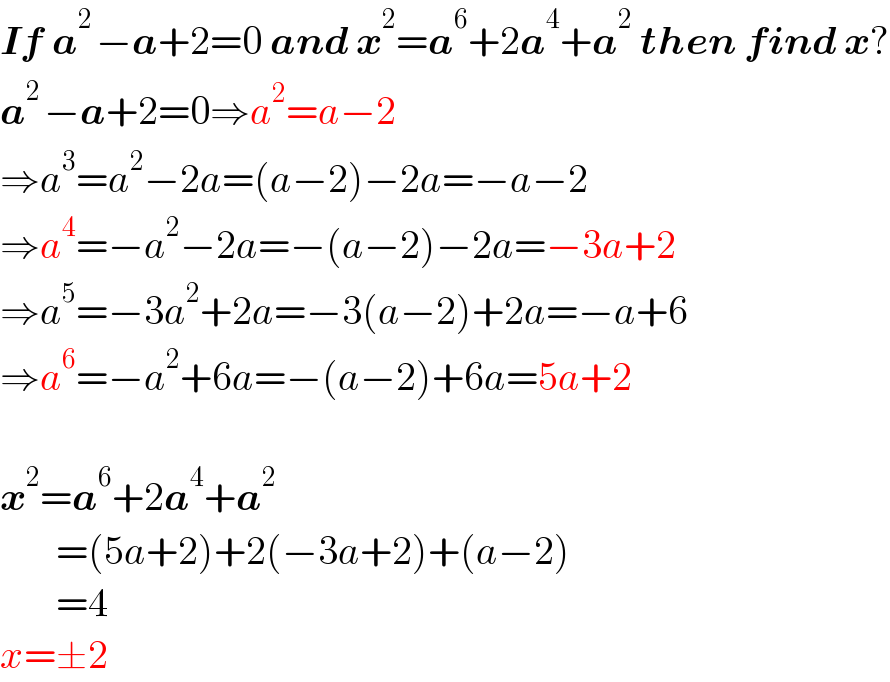
If a^(2 ) −a+2=0 and x^2 =a^6 +2a^4 +a^2 then find x? a^(2 ) −a+2=0⇒a^2 =a−2 ⇒a^3 =a^2 −2a=(a−2)−2a=−a−2 ⇒a^4 =−a^2 −2a=−(a−2)−2a=−3a+2 ⇒a^5 =−3a^2 +2a=−3(a−2)+2a=−a+6 ⇒a^6 =−a^2 +6a=−(a−2)+6a=5a+2 x^2 =a^6 +2a^4 +a^2 =(5a+2)+2(−3a+2)+(a−2) =4 x=±2

$$\boldsymbol{{If}}\:\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\:\boldsymbol{{and}}\:\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{a}}^{\mathrm{6}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{4}} +\boldsymbol{{a}}^{\mathrm{2}} \:\boldsymbol{{then}}\:\boldsymbol{{find}}\:\boldsymbol{{x}}? \\ $$$$\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\Rightarrow{a}^{\mathrm{2}} ={a}−\mathrm{2} \\ $$$$\Rightarrow{a}^{\mathrm{3}} ={a}^{\mathrm{2}} −\mathrm{2}{a}=\left({a}−\mathrm{2}\right)−\mathrm{2}{a}=−{a}−\mathrm{2} \\ $$$$\Rightarrow{a}^{\mathrm{4}} =−{a}^{\mathrm{2}} −\mathrm{2}{a}=−\left({a}−\mathrm{2}\right)−\mathrm{2}{a}=−\mathrm{3}{a}+\mathrm{2} \\ $$$$\Rightarrow{a}^{\mathrm{5}} =−\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{a}=−\mathrm{3}\left({a}−\mathrm{2}\right)+\mathrm{2}{a}=−{a}+\mathrm{6} \\ $$$$\Rightarrow{a}^{\mathrm{6}} =−{a}^{\mathrm{2}} +\mathrm{6}{a}=−\left({a}−\mathrm{2}\right)+\mathrm{6}{a}=\mathrm{5}{a}+\mathrm{2} \\ $$$$ \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{a}}^{\mathrm{6}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{4}} +\boldsymbol{{a}}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{5}{a}+\mathrm{2}\right)+\mathrm{2}\left(−\mathrm{3}{a}+\mathrm{2}\right)+\left({a}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{4} \\ $$$${x}=\pm\mathrm{2} \\ $$

Commented by siyathokoza last updated on 06/Feb/24

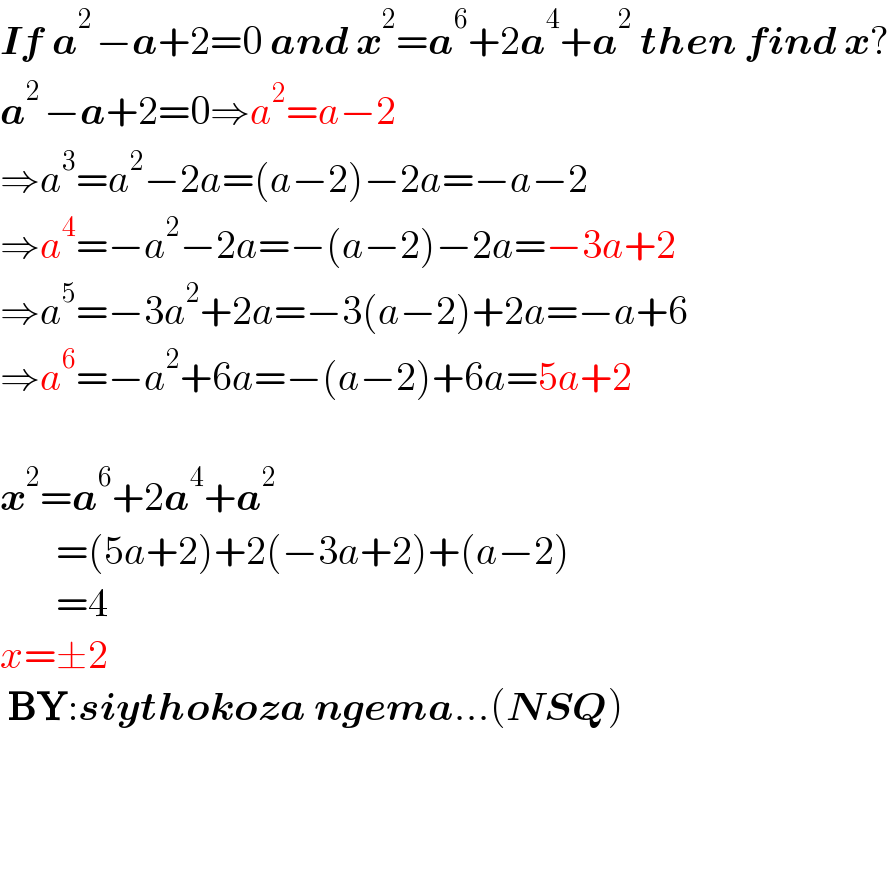
If a^(2 ) −a+2=0 and x^2 =a^6 +2a^4 +a^2 then find x? a^(2 ) −a+2=0⇒a^2 =a−2 ⇒a^3 =a^2 −2a=(a−2)−2a=−a−2 ⇒a^4 =−a^2 −2a=−(a−2)−2a=−3a+2 ⇒a^5 =−3a^2 +2a=−3(a−2)+2a=−a+6 ⇒a^6 =−a^2 +6a=−(a−2)+6a=5a+2 x^2 =a^6 +2a^4 +a^2 =(5a+2)+2(−3a+2)+(a−2) =4 x=±2 BY:siythokoza ngema...(NSQ)

$$\boldsymbol{{If}}\:\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\:\boldsymbol{{and}}\:\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{a}}^{\mathrm{6}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{4}} +\boldsymbol{{a}}^{\mathrm{2}} \:\boldsymbol{{then}}\:\boldsymbol{{find}}\:\boldsymbol{{x}}? \\ $$$$\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\Rightarrow{a}^{\mathrm{2}} ={a}−\mathrm{2} \\ $$$$\Rightarrow{a}^{\mathrm{3}} ={a}^{\mathrm{2}} −\mathrm{2}{a}=\left({a}−\mathrm{2}\right)−\mathrm{2}{a}=−{a}−\mathrm{2} \\ $$$$\Rightarrow{a}^{\mathrm{4}} =−{a}^{\mathrm{2}} −\mathrm{2}{a}=−\left({a}−\mathrm{2}\right)−\mathrm{2}{a}=−\mathrm{3}{a}+\mathrm{2} \\ $$$$\Rightarrow{a}^{\mathrm{5}} =−\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{a}=−\mathrm{3}\left({a}−\mathrm{2}\right)+\mathrm{2}{a}=−{a}+\mathrm{6} \\ $$$$\Rightarrow{a}^{\mathrm{6}} =−{a}^{\mathrm{2}} +\mathrm{6}{a}=−\left({a}−\mathrm{2}\right)+\mathrm{6}{a}=\mathrm{5}{a}+\mathrm{2} \\ $$$$ \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{a}}^{\mathrm{6}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{4}} +\boldsymbol{{a}}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{5}{a}+\mathrm{2}\right)+\mathrm{2}\left(−\mathrm{3}{a}+\mathrm{2}\right)+\left({a}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{4} \\ $$$${x}=\pm\mathrm{2} \\ $$$$\:\boldsymbol{\mathrm{BY}}:\boldsymbol{{siythokoza}}\:\boldsymbol{{ngema}}...\left(\boldsymbol{{NSQ}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 02/Feb/24

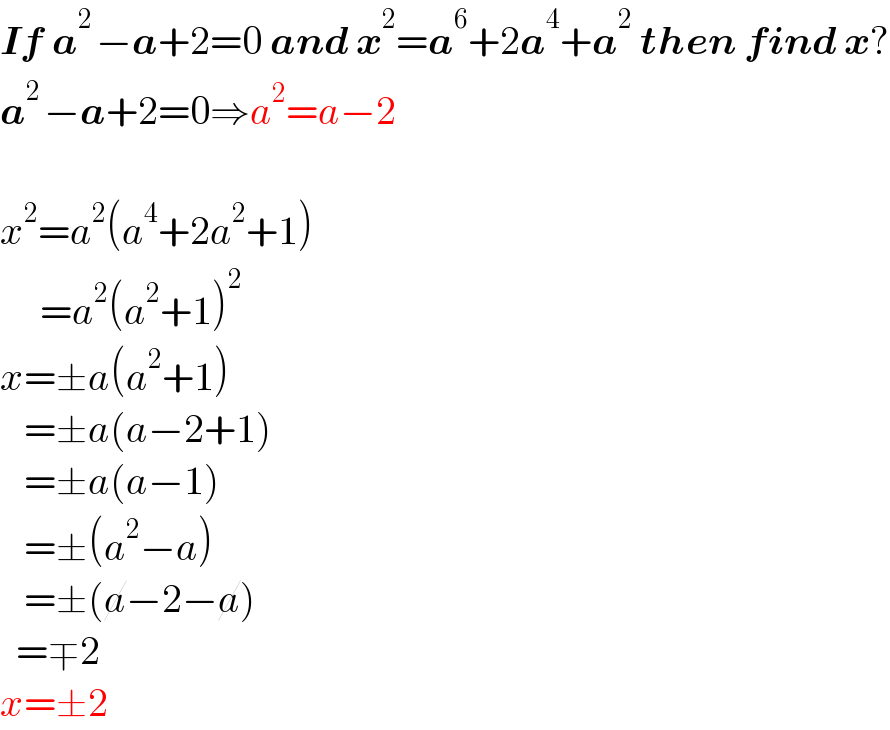
If a^(2 ) −a+2=0 and x^2 =a^6 +2a^4 +a^2 then find x? a^(2 ) −a+2=0⇒a^2 =a−2 x^2 =a^2 (a^4 +2a^2 +1) =a^2 (a^2 +1)^2 x=±a(a^2 +1) =±a(a−2+1) =±a(a−1) =±(a^2 −a) =±(a−2−a) =∓2 x=±2

$$\boldsymbol{{If}}\:\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\:\boldsymbol{{and}}\:\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{a}}^{\mathrm{6}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{4}} +\boldsymbol{{a}}^{\mathrm{2}} \:\boldsymbol{{then}}\:\boldsymbol{{find}}\:\boldsymbol{{x}}? \\ $$$$\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\Rightarrow{a}^{\mathrm{2}} ={a}−\mathrm{2} \\ $$$$\: \\ $$$${x}^{\mathrm{2}} ={a}^{\mathrm{2}} \left({a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\:={a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$${x}=\pm{a}\left({a}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:\:\:=\pm{a}\left({a}−\mathrm{2}+\mathrm{1}\right) \\ $$$$\:\:\:=\pm{a}\left({a}−\mathrm{1}\right) \\ $$$$\:\:\:=\pm\left({a}^{\mathrm{2}} −{a}\right) \\ $$$$\:\:\:=\pm\left(\cancel{{a}}−\mathrm{2}−\cancel{{a}}\right) \\ $$$$\:\:=\mp\mathrm{2} \\ $$$${x}=\pm\mathrm{2} \\ $$

Commented by Panav last updated on 10/Feb/24

Correct

$${Correct} \\ $$

Answered by Rasheed.Sindhi last updated on 02/Feb/24

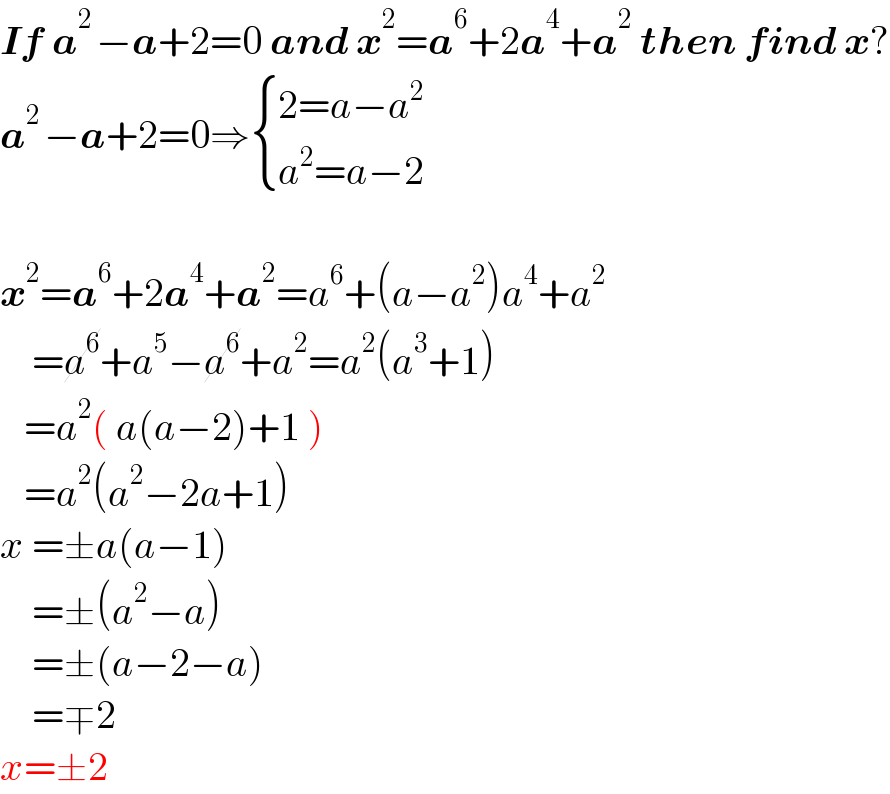
If a^(2 ) −a+2=0 and x^2 =a^6 +2a^4 +a^2 then find x? a^(2 ) −a+2=0⇒ { ((2=a−a^2 )),((a^2 =a−2)) :} x^2 =a^6 +2a^4 +a^2 =a^6 +(a−a^2 )a^4 +a^2 =a^6 +a^5 −a^6 +a^2 =a^2 (a^3 +1) =a^2 ( a(a−2)+1 ) =a^2 (a^2 −2a+1) x =±a(a−1) =±(a^2 −a) =±(a−2−a) =∓2 x=±2

$$\boldsymbol{{If}}\:\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\:\boldsymbol{{and}}\:\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{a}}^{\mathrm{6}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{4}} +\boldsymbol{{a}}^{\mathrm{2}} \:\boldsymbol{{then}}\:\boldsymbol{{find}}\:\boldsymbol{{x}}? \\ $$$$\boldsymbol{{a}}^{\mathrm{2}\:} −\boldsymbol{{a}}+\mathrm{2}=\mathrm{0}\Rightarrow\begin{cases}{\mathrm{2}={a}−{a}^{\mathrm{2}} }\\{{a}^{\mathrm{2}} ={a}−\mathrm{2}}\end{cases} \\ $$$$\: \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{a}}^{\mathrm{6}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{4}} +\boldsymbol{{a}}^{\mathrm{2}} ={a}^{\mathrm{6}} +\left({a}−{a}^{\mathrm{2}} \right){a}^{\mathrm{4}} +{a}^{\mathrm{2}} \\ $$$$\:\:\:\:=\cancel{{a}^{\mathrm{6}} }+{a}^{\mathrm{5}} −\cancel{{a}^{\mathrm{6}} }+{a}^{\mathrm{2}} ={a}^{\mathrm{2}} \left({a}^{\mathrm{3}} +\mathrm{1}\right) \\ $$$$\:\:\:={a}^{\mathrm{2}} \left(\:{a}\left({a}−\mathrm{2}\right)+\mathrm{1}\:\right) \\ $$$$\:\:\:={a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}\right) \\ $$$${x}\:=\pm{a}\left({a}−\mathrm{1}\right) \\ $$$$\:\:\:\:=\pm\left({a}^{\mathrm{2}} −{a}\right) \\ $$$$\:\:\:\:=\pm\left({a}−\mathrm{2}−{a}\right) \\ $$$$\:\:\:\:=\mp\mathrm{2} \\ $$$${x}=\pm\mathrm{2} \\ $$

Answered by deleteduser1 last updated on 02/Feb/24

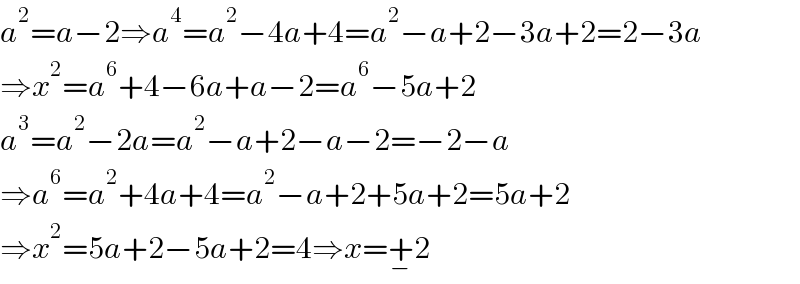
a^2 =a−2⇒a^4 =a^2 −4a+4=a^2 −a+2−3a+2=2−3a ⇒x^2 =a^6 +4−6a+a−2=a^6 −5a+2 a^3 =a^2 −2a=a^2 −a+2−a−2=−2−a ⇒a^6 =a^2 +4a+4=a^2 −a+2+5a+2=5a+2 ⇒x^2 =5a+2−5a+2=4⇒x=+_− 2

$${a}^{\mathrm{2}} ={a}−\mathrm{2}\Rightarrow{a}^{\mathrm{4}} ={a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{4}={a}^{\mathrm{2}} −{a}+\mathrm{2}−\mathrm{3}{a}+\mathrm{2}=\mathrm{2}−\mathrm{3}{a} \\ $$$$\Rightarrow{x}^{\mathrm{2}} ={a}^{\mathrm{6}} +\mathrm{4}−\mathrm{6}{a}+{a}−\mathrm{2}={a}^{\mathrm{6}} −\mathrm{5}{a}+\mathrm{2} \\ $$$${a}^{\mathrm{3}} ={a}^{\mathrm{2}} −\mathrm{2}{a}={a}^{\mathrm{2}} −{a}+\mathrm{2}−{a}−\mathrm{2}=−\mathrm{2}−{a} \\ $$$$\Rightarrow{a}^{\mathrm{6}} ={a}^{\mathrm{2}} +\mathrm{4}{a}+\mathrm{4}={a}^{\mathrm{2}} −{a}+\mathrm{2}+\mathrm{5}{a}+\mathrm{2}=\mathrm{5}{a}+\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{5}{a}+\mathrm{2}−\mathrm{5}{a}+\mathrm{2}=\mathrm{4}\Rightarrow{x}=\underset{−} {+}\mathrm{2} \\ $$

Answered by esmaeil last updated on 02/Feb/24

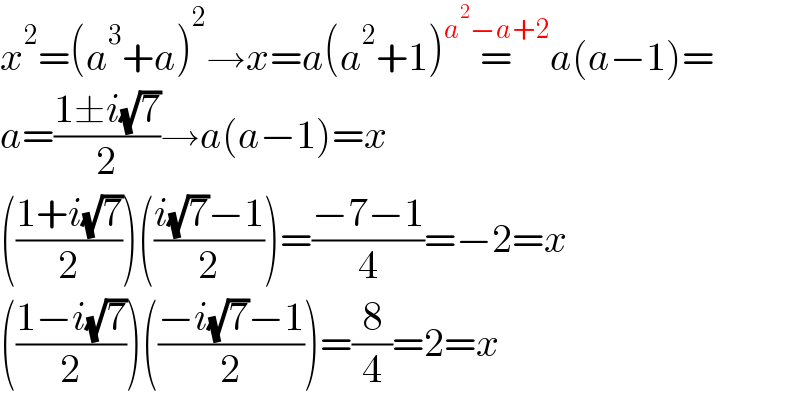
x^2 =(a^3 +a)^2 →x=a(a^2 +1)=^(a^2 −a+2) a(a−1)= a=((1±i(√7))/2)→a(a−1)=x (((1+i(√7))/2))(((i(√7)−1)/2))=((−7−1)/4)=−2=x (((1−i(√7))/2))(((−i(√7)−1)/2))=(8/4)=2=x

$${x}^{\mathrm{2}} =\left({a}^{\mathrm{3}} +{a}\right)^{\mathrm{2}} \rightarrow{x}={a}\left({a}^{\mathrm{2}} +\mathrm{1}\right)\overset{{a}^{\mathrm{2}} −{a}+\mathrm{2}} {=}{a}\left({a}−\mathrm{1}\right)= \\ $$$${a}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\rightarrow{a}\left({a}−\mathrm{1}\right)={x} \\ $$$$\left(\frac{\mathrm{1}+{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\right)\left(\frac{{i}\sqrt{\mathrm{7}}−\mathrm{1}}{\mathrm{2}}\right)=\frac{−\mathrm{7}−\mathrm{1}}{\mathrm{4}}=−\mathrm{2}={x} \\ $$$$\left(\frac{\mathrm{1}−{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\right)\left(\frac{−{i}\sqrt{\mathrm{7}}−\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{8}}{\mathrm{4}}=\mathrm{2}={x} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com