Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 191553 by MATHEMATICSAM last updated on 25/Apr/23

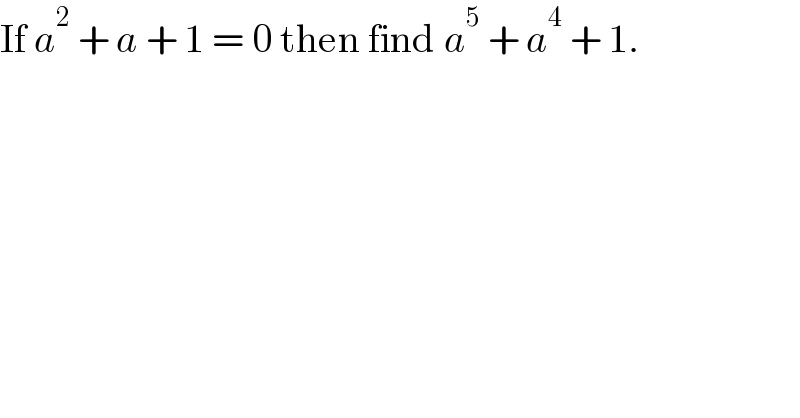
If a^2 + a + 1 = 0 then find a^5 + a^4 + 1.

$$\mathrm{If}\:{a}^{\mathrm{2}} \:+\:{a}\:+\:\mathrm{1}\:=\:\mathrm{0}\:\mathrm{then}\:\mathrm{find}\:{a}^{\mathrm{5}} \:+\:{a}^{\mathrm{4}} \:+\:\mathrm{1}. \\ $$

Commented by Tinku Tara last updated on 25/Apr/23

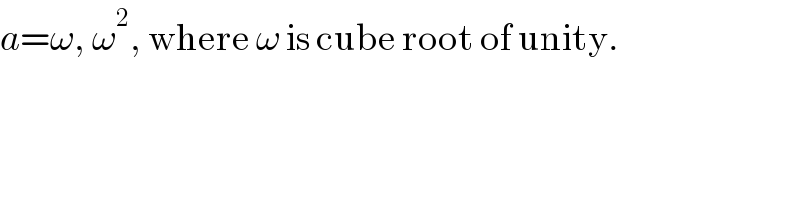
a=ω, ω^2 , where ω is cube root of unity.

$${a}=\omega,\:\omega^{\mathrm{2}} ,\:\mathrm{where}\:\omega\:\mathrm{is}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}. \\ $$

Answered by manxsol last updated on 27/Apr/23

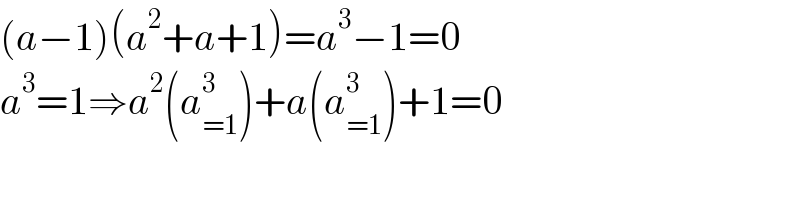
(a−1)(a^2 +a+1)=a^3 −1=0 a^3 =1⇒a^2 (a_(=1) ^3 )+a(a_(=1) ^3 )+1=0

$$\left({a}−\mathrm{1}\right)\left({a}^{\mathrm{2}} +{a}+\mathrm{1}\right)={a}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$${a}^{\mathrm{3}} =\mathrm{1}\Rightarrow{a}^{\mathrm{2}} \left({a}_{=\mathrm{1}} ^{\mathrm{3}} \right)+{a}\left({a}_{=\mathrm{1}} ^{\mathrm{3}} \right)+\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$

Answered by mr W last updated on 25/Apr/23

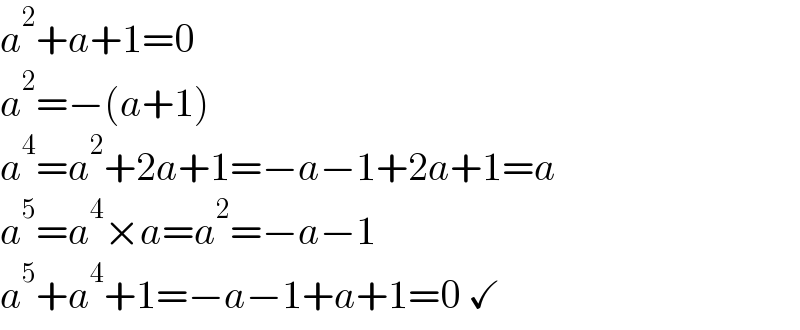
a^2 +a+1=0 a^2 =−(a+1) a^4 =a^2 +2a+1=−a−1+2a+1=a a^5 =a^4 ×a=a^2 =−a−1 a^5 +a^4 +1=−a−1+a+1=0 ✓

$${a}^{\mathrm{2}} +{a}+\mathrm{1}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} =−\left({a}+\mathrm{1}\right) \\ $$$${a}^{\mathrm{4}} ={a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}=−{a}−\mathrm{1}+\mathrm{2}{a}+\mathrm{1}={a} \\ $$$${a}^{\mathrm{5}} ={a}^{\mathrm{4}} ×{a}={a}^{\mathrm{2}} =−{a}−\mathrm{1} \\ $$$${a}^{\mathrm{5}} +{a}^{\mathrm{4}} +\mathrm{1}=−{a}−\mathrm{1}+{a}+\mathrm{1}=\mathrm{0}\:\checkmark \\ $$

Answered by Rasheed.Sindhi last updated on 26/Apr/23

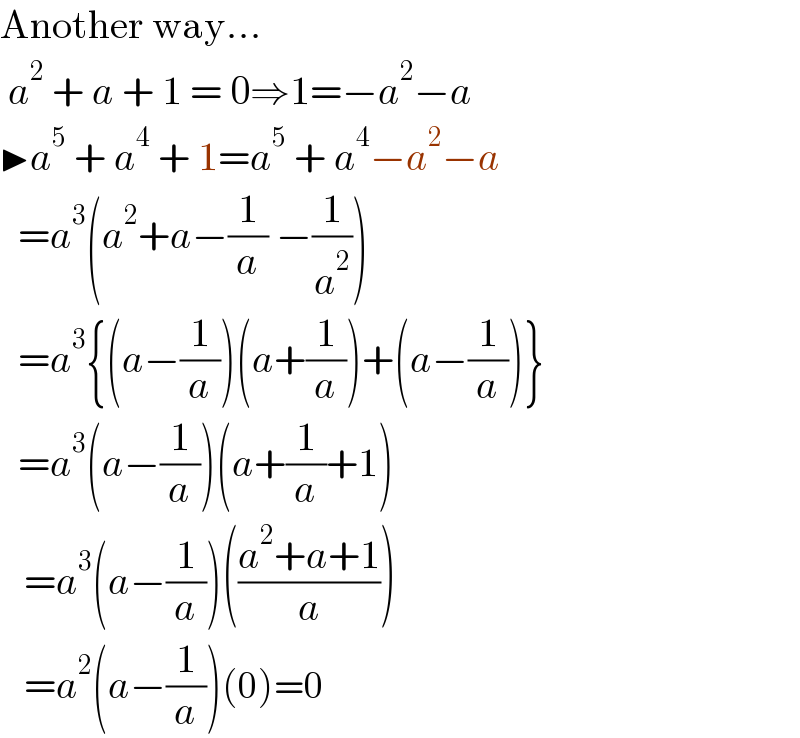
Another way... a^2 + a + 1 = 0⇒1=−a^2 −a ▶a^5 + a^4 + 1=a^5 + a^4 −a^2 −a =a^3 (a^2 +a−(1/a) −(1/a^2 )) =a^3 {(a−(1/a))(a+(1/a))+(a−(1/a))} =a^3 (a−(1/a))(a+(1/a)+1) =a^3 (a−(1/a))(((a^2 +a+1)/a)) =a^2 (a−(1/a))(0)=0

$$\mathrm{Another}\:\mathrm{way}... \\ $$$$\:{a}^{\mathrm{2}} \:+\:{a}\:+\:\mathrm{1}\:=\:\mathrm{0}\Rightarrow\mathrm{1}=−{a}^{\mathrm{2}} −{a} \\ $$$$\blacktriangleright{a}^{\mathrm{5}} \:+\:{a}^{\mathrm{4}} \:+\:\mathrm{1}={a}^{\mathrm{5}} \:+\:{a}^{\mathrm{4}} −{a}^{\mathrm{2}} −{a} \\ $$$$\:\:\:={a}^{\mathrm{3}} \left({a}^{\mathrm{2}} +{a}−\frac{\mathrm{1}}{{a}}\:−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right) \\ $$$$\:\:\:={a}^{\mathrm{3}} \left\{\left({a}−\frac{\mathrm{1}}{{a}}\right)\left({a}+\frac{\mathrm{1}}{{a}}\right)+\left({a}−\frac{\mathrm{1}}{{a}}\right)\right\} \\ $$$$\:\:\:={a}^{\mathrm{3}} \left({a}−\frac{\mathrm{1}}{{a}}\right)\left({a}+\frac{\mathrm{1}}{{a}}+\mathrm{1}\right) \\ $$$$\:\:\:\:={a}^{\mathrm{3}} \left({a}−\frac{\mathrm{1}}{{a}}\right)\left(\frac{{a}^{\mathrm{2}} +{a}+\mathrm{1}}{{a}}\right) \\ $$$$\:\:\:\:={a}^{\mathrm{2}} \left({a}−\frac{\mathrm{1}}{{a}}\right)\left(\mathrm{0}\right)=\mathrm{0} \\ $$

Answered by Tinku Tara last updated on 05/Jul/23

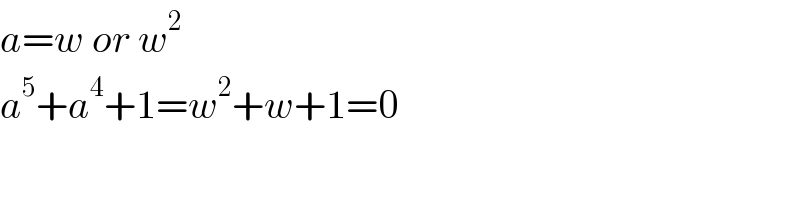
a=w or w^2 a^5 +a^4 +1=w^2 +w+1=0

$${a}={w}\:{or}\:{w}^{\mathrm{2}} \\ $$$${a}^{\mathrm{5}} +{a}^{\mathrm{4}} +\mathrm{1}={w}^{\mathrm{2}} +{w}+\mathrm{1}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com