
Question Number 130581 by bramlexs22 last updated on 27/Jan/21

$$\mathrm{If}\:\mathrm{a}_{\mathrm{1}} ,\mathrm{a}_{\mathrm{2}} \:,\mathrm{a}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{in}\:\mathrm{AP}\:\mathrm{and}\:\mathrm{d}\:\mathrm{is}\:\mathrm{the}\:\mathrm{common} \\ $$$$\mathrm{difference}\:\mathrm{then}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{d}}{\mathrm{1}+\mathrm{a}_{\mathrm{1}} \mathrm{a}_{\mathrm{2}} }\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{d}}{\mathrm{1}+\mathrm{a}_{\mathrm{2}} \mathrm{a}_{\mathrm{3}} }\right)=? \\ $$
Answered by som(math1967) last updated on 27/Jan/21
![tan^(−1) (((a_2 −a_1 )/(1+a_1 a_2 )))+tan^(−1) (((a_3 −a_2 )/(1+a_2 −a_3 ))) =tan^(−1) a_2 −tan^(−1) a_1 +tan^(−1) a_3 −tan^(−1) a_2 =tan^(−1) a_3 −tan^(−1) a_1 [d=a_2 −a_1 =a_3 −a_2 ]](Q130583.png)
$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}_{\mathrm{2}} −{a}_{\mathrm{1}} }{\mathrm{1}+{a}_{\mathrm{1}} {a}_{\mathrm{2}} }\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}_{\mathrm{3}} −{a}_{\mathrm{2}} }{\mathrm{1}+{a}_{\mathrm{2}} −{a}_{\mathrm{3}} }\right) \\ $$$$=\mathrm{tan}^{−\mathrm{1}} {a}_{\mathrm{2}} −\mathrm{tan}^{−\mathrm{1}} {a}_{\mathrm{1}} +\mathrm{tan}^{−\mathrm{1}} {a}_{\mathrm{3}} −\mathrm{tan}^{−\mathrm{1}} {a}_{\mathrm{2}} \\ $$$$=\mathrm{tan}^{−\mathrm{1}} {a}_{\mathrm{3}} −\mathrm{tan}^{−\mathrm{1}} {a}_{\mathrm{1}} \\ $$$$\left[{d}={a}_{\mathrm{2}} −{a}_{\mathrm{1}} ={a}_{\mathrm{3}} −{a}_{\mathrm{2}} \right] \\ $$
Commented by bramlexs22 last updated on 27/Jan/21

Commented by bramlexs22 last updated on 27/Jan/21
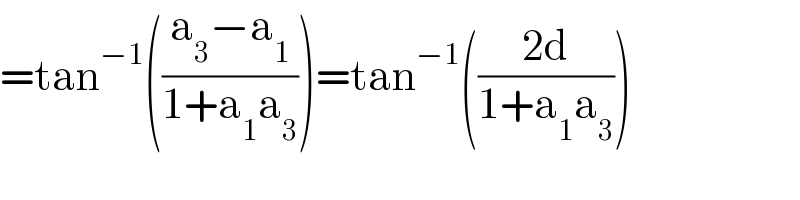
$$=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{a}_{\mathrm{3}} −\mathrm{a}_{\mathrm{1}} }{\mathrm{1}+\mathrm{a}_{\mathrm{1}} \mathrm{a}_{\mathrm{3}} }\right)=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2d}}{\mathrm{1}+\mathrm{a}_{\mathrm{1}} \mathrm{a}_{\mathrm{3}} }\right) \\ $$
