
Question Number 128368 by I want to learn more last updated on 06/Jan/21
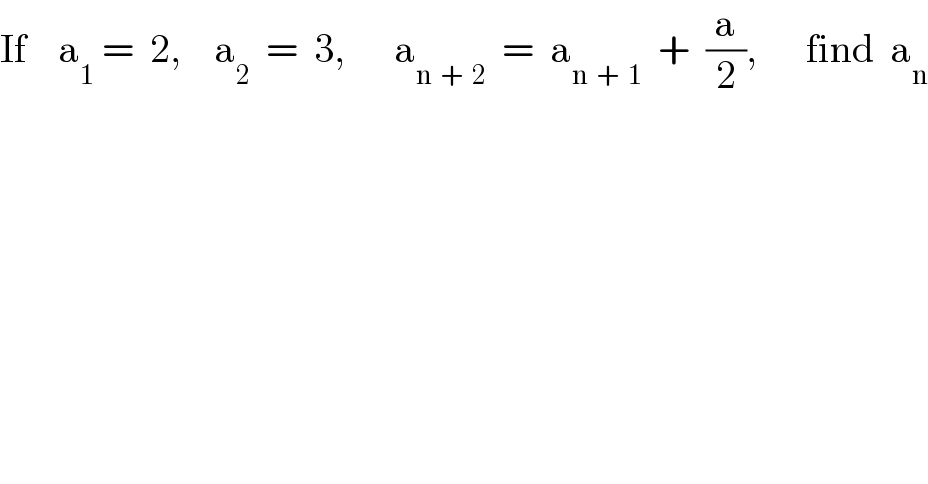
$$\mathrm{If}\:\:\:\:\mathrm{a}_{\mathrm{1}} \:=\:\:\mathrm{2},\:\:\:\:\mathrm{a}_{\mathrm{2}} \:\:=\:\:\mathrm{3},\:\:\:\:\:\:\mathrm{a}_{\mathrm{n}\:\:+\:\:\mathrm{2}} \:\:=\:\:\mathrm{a}_{\mathrm{n}\:\:+\:\:\mathrm{1}} \:\:+\:\:\frac{\mathrm{a}}{\mathrm{2}},\:\:\:\:\:\:\mathrm{find}\:\:\mathrm{a}_{\mathrm{n}} \\ $$
Answered by mr W last updated on 06/Jan/21
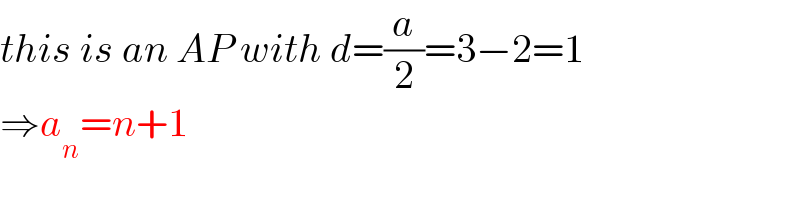
$${this}\:{is}\:{an}\:{AP}\:{with}\:{d}=\frac{{a}}{\mathrm{2}}=\mathrm{3}−\mathrm{2}=\mathrm{1} \\ $$$$\Rightarrow{a}_{{n}} ={n}+\mathrm{1} \\ $$
Commented by I want to learn more last updated on 06/Jan/21

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 06/Jan/21
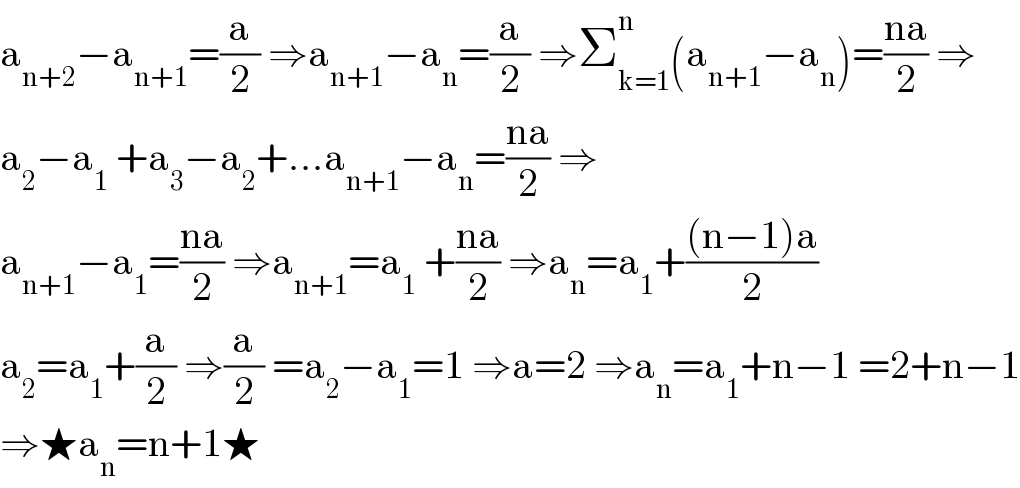
$$\mathrm{a}_{\mathrm{n}+\mathrm{2}} −\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{a}}{\mathrm{2}}\:\Rightarrow\mathrm{a}_{\mathrm{n}+\mathrm{1}} −\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{a}}{\mathrm{2}}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{a}_{\mathrm{n}+\mathrm{1}} −\mathrm{a}_{\mathrm{n}} \right)=\frac{\mathrm{na}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{a}_{\mathrm{2}} −\mathrm{a}_{\mathrm{1}} \:+\mathrm{a}_{\mathrm{3}} −\mathrm{a}_{\mathrm{2}} +...\mathrm{a}_{\mathrm{n}+\mathrm{1}} −\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{na}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{a}_{\mathrm{n}+\mathrm{1}} −\mathrm{a}_{\mathrm{1}} =\frac{\mathrm{na}}{\mathrm{2}}\:\Rightarrow\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\mathrm{a}_{\mathrm{1}} \:+\frac{\mathrm{na}}{\mathrm{2}}\:\Rightarrow\mathrm{a}_{\mathrm{n}} =\mathrm{a}_{\mathrm{1}} +\frac{\left(\mathrm{n}−\mathrm{1}\right)\mathrm{a}}{\mathrm{2}} \\ $$$$\mathrm{a}_{\mathrm{2}} =\mathrm{a}_{\mathrm{1}} +\frac{\mathrm{a}}{\mathrm{2}}\:\Rightarrow\frac{\mathrm{a}}{\mathrm{2}}\:=\mathrm{a}_{\mathrm{2}} −\mathrm{a}_{\mathrm{1}} =\mathrm{1}\:\Rightarrow\mathrm{a}=\mathrm{2}\:\Rightarrow\mathrm{a}_{\mathrm{n}} =\mathrm{a}_{\mathrm{1}} +\mathrm{n}−\mathrm{1}\:=\mathrm{2}+\mathrm{n}−\mathrm{1} \\ $$$$\Rightarrow\bigstar\mathrm{a}_{\mathrm{n}} =\mathrm{n}+\mathrm{1}\bigstar \\ $$
Commented by I want to learn more last updated on 07/Jan/21

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
