
Question Number 114676 by ZiYangLee last updated on 20/Sep/20
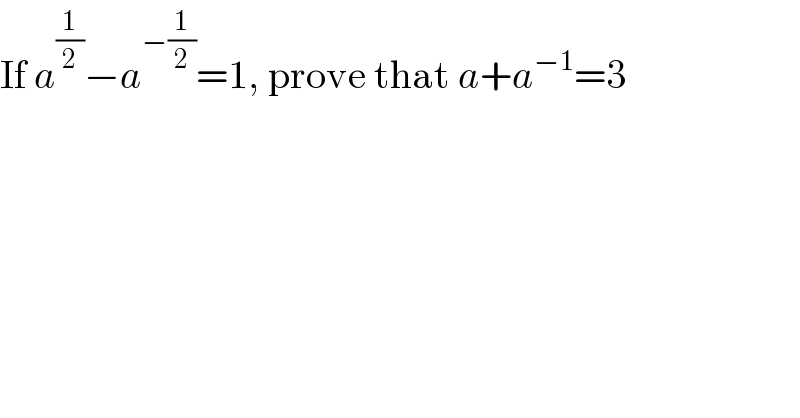
$$\mathrm{If}\:{a}^{\frac{\mathrm{1}}{\mathrm{2}}} −{a}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1},\:\mathrm{prove}\:\mathrm{that}\:{a}+{a}^{−\mathrm{1}} =\mathrm{3} \\ $$
Answered by Olaf last updated on 20/Sep/20
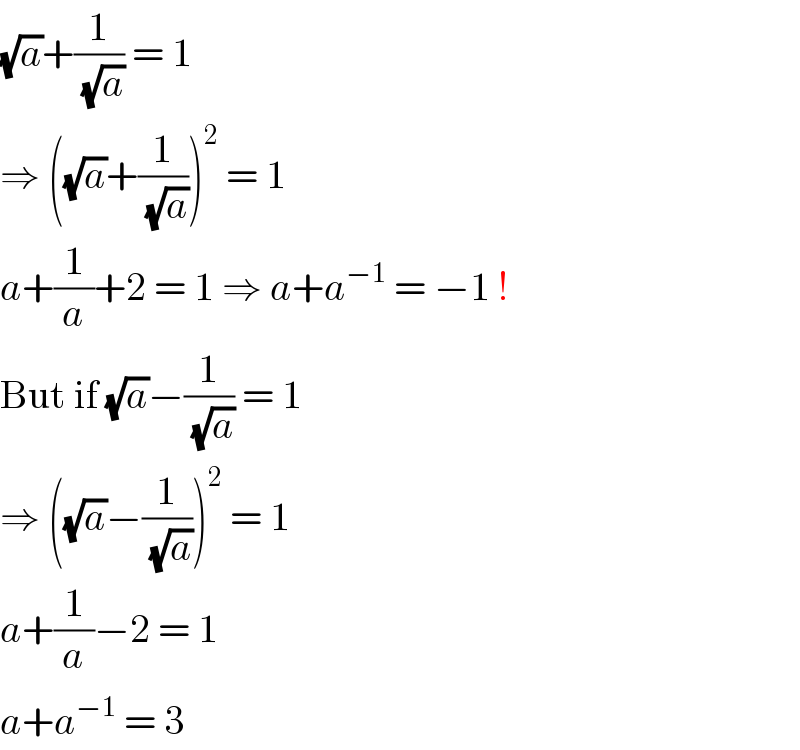
$$\sqrt{{a}}+\frac{\mathrm{1}}{\:\sqrt{{a}}}\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\left(\sqrt{{a}}+\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$${a}+\frac{\mathrm{1}}{{a}}+\mathrm{2}\:=\:\mathrm{1}\:\Rightarrow\:{a}+{a}^{−\mathrm{1}} \:=\:−\mathrm{1}\:! \\ $$$$\mathrm{But}\:\mathrm{if}\:\sqrt{{a}}−\frac{\mathrm{1}}{\:\sqrt{{a}}}\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\left(\sqrt{{a}}−\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$${a}+\frac{\mathrm{1}}{{a}}−\mathrm{2}\:=\:\mathrm{1} \\ $$$${a}+{a}^{−\mathrm{1}} \:=\:\mathrm{3} \\ $$
Commented by ZiYangLee last updated on 20/Sep/20
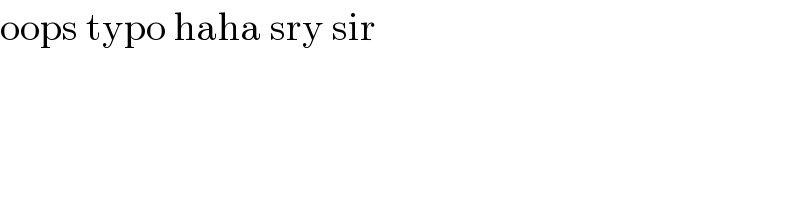
$$\mathrm{oops}\:\mathrm{typo}\:\mathrm{haha}\:\mathrm{sry}\:\mathrm{sir} \\ $$
