Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 75327 by TawaTawa last updated on 09/Dec/19

If T_(n + 1) = 1 + (1/2)T_n Find a formular for T_n in terms of n and find the sum of first n terms

$$\mathrm{If}\:\:\:\:\:\mathrm{T}_{\mathrm{n}\:+\:\mathrm{1}} \:\:\:=\:\:\:\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{T}_{\mathrm{n}} \\ $$$$\mathrm{Find}\:\mathrm{a}\:\mathrm{formular}\:\mathrm{for}\:\:\mathrm{T}_{\mathrm{n}} \:\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\:\mathrm{n} \\ $$$$\mathrm{and}\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{first}\:\mathrm{n}\:\mathrm{terms} \\ $$

Commented by malwaan last updated on 11/Dec/19

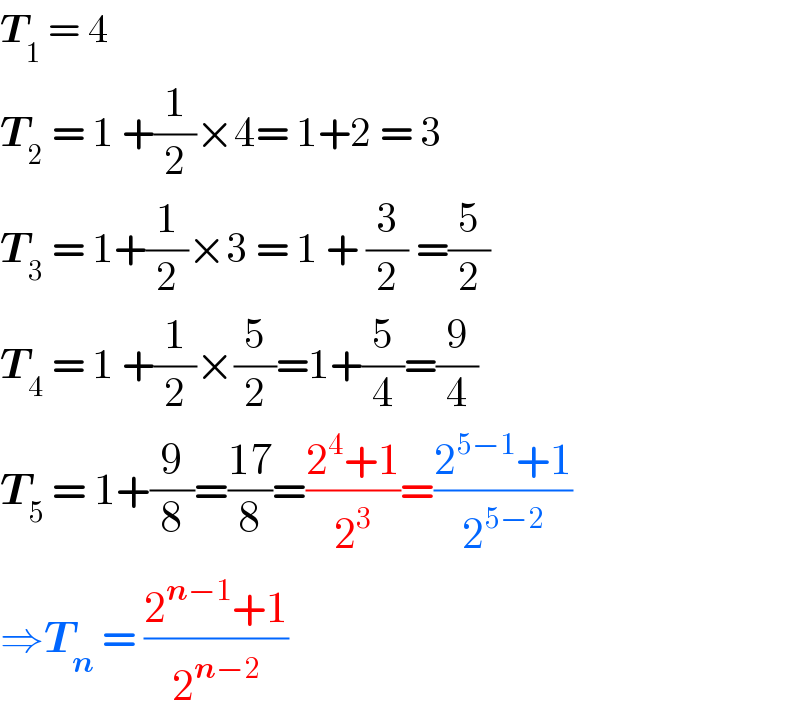
T_1 = 4 T_2 = 1 +(1/2)×4= 1+2 = 3 T_3 = 1+(1/2)×3 = 1 + (3/2) =(5/2) T_4 = 1 +(1/2)×(5/2)=1+(5/4)=(9/4) T_5 = 1+(9/8)=((17)/8)=((2^4 +1)/2^3 )=((2^(5−1) +1)/2^(5−2) ) ⇒T_n = ((2^(n−1) +1)/2^(n−2) )

$$\boldsymbol{{T}}_{\mathrm{1}} \:=\:\mathrm{4} \\ $$$$\boldsymbol{{T}}_{\mathrm{2}} \:=\:\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}=\:\mathrm{1}+\mathrm{2}\:=\:\mathrm{3} \\ $$$$\boldsymbol{{T}}_{\mathrm{3}} \:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{3}\:=\:\mathrm{1}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\boldsymbol{{T}}_{\mathrm{4}} \:=\:\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{1}+\frac{\mathrm{5}}{\mathrm{4}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\boldsymbol{{T}}_{\mathrm{5}} \:=\:\mathrm{1}+\frac{\mathrm{9}}{\mathrm{8}}=\frac{\mathrm{17}}{\mathrm{8}}=\frac{\mathrm{2}^{\mathrm{4}} +\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }=\frac{\mathrm{2}^{\mathrm{5}−\mathrm{1}} +\mathrm{1}}{\mathrm{2}^{\mathrm{5}−\mathrm{2}} } \\ $$$$\Rightarrow\boldsymbol{{T}}_{\boldsymbol{{n}}} \:=\:\frac{\mathrm{2}^{\boldsymbol{{n}}−\mathrm{1}} +\mathrm{1}}{\mathrm{2}^{\boldsymbol{{n}}−\mathrm{2}} } \\ $$

Commented by mr W last updated on 10/Dec/19

please check the question: when giving a recursive sequence, the first term T_1 must be given in order to determine all terms.

$${please}\:{check}\:{the}\:{question}: \\ $$$${when}\:{giving}\:{a}\:{recursive}\:{sequence}, \\ $$$${the}\:{first}\:{term}\:{T}_{\mathrm{1}} \:{must}\:{be}\:{given}\:{in} \\ $$$${order}\:{to}\:{determine}\:{all}\:{terms}. \\ $$

Commented by TawaTawa last updated on 10/Dec/19

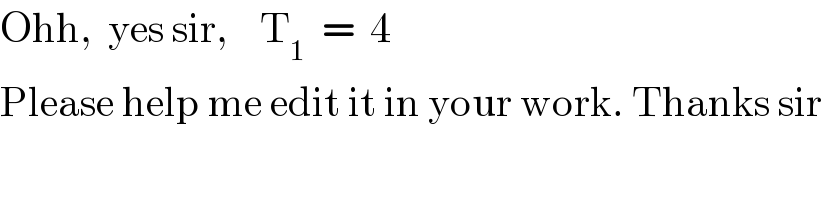
Ohh, yes sir, T_1 = 4 Please help me edit it in your work. Thanks sir

$$\mathrm{Ohh},\:\:\mathrm{yes}\:\mathrm{sir},\:\:\:\:\mathrm{T}_{\mathrm{1}} \:\:=\:\:\mathrm{4} \\ $$$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{edit}\:\mathrm{it}\:\mathrm{in}\:\mathrm{your}\:\mathrm{work}.\:\mathrm{Thanks}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 10/Dec/19

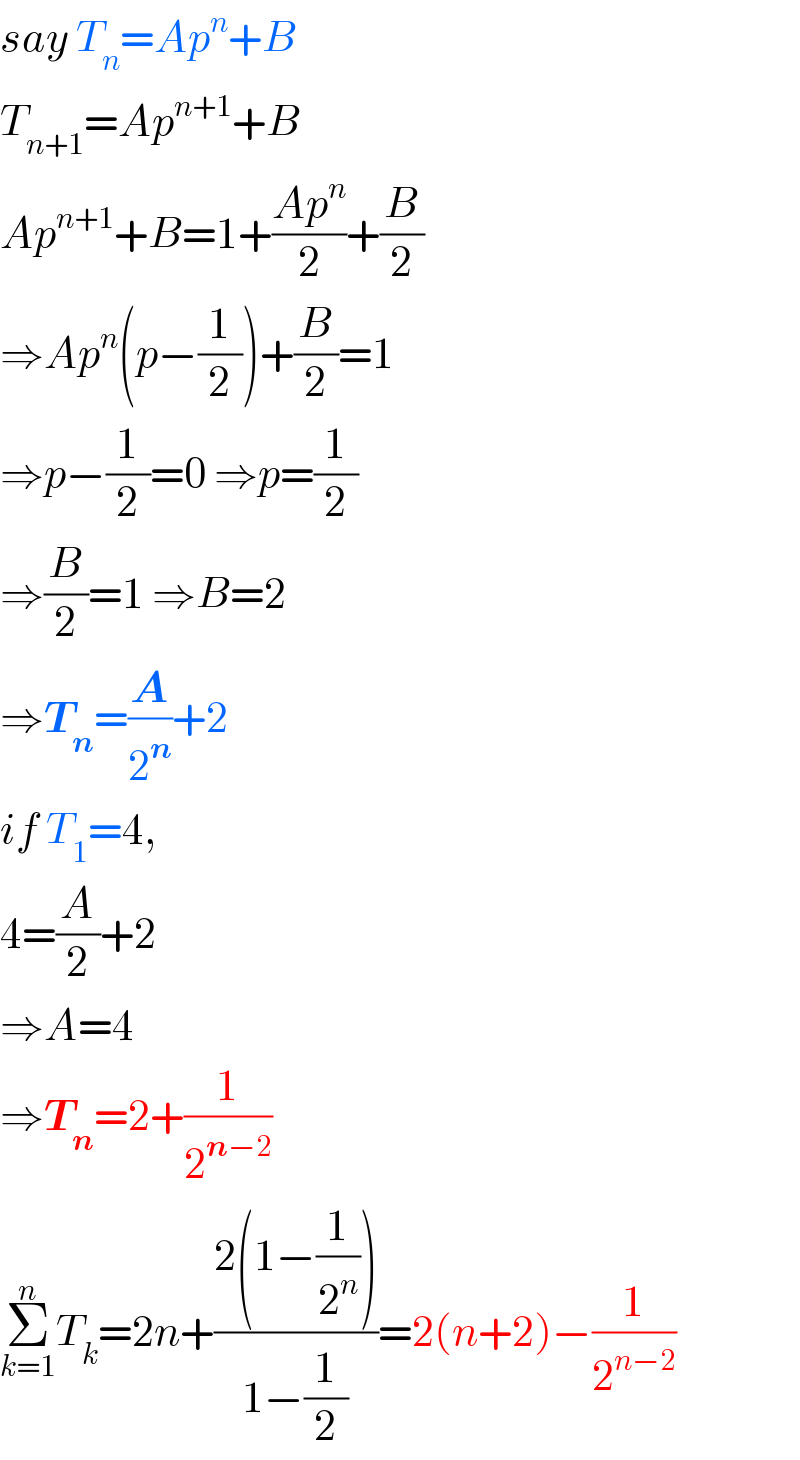
say T_n =Ap^n +B T_(n+1) =Ap^(n+1) +B Ap^(n+1) +B=1+((Ap^n )/2)+(B/2) ⇒Ap^n (p−(1/2))+(B/2)=1 ⇒p−(1/2)=0 ⇒p=(1/2) ⇒(B/2)=1 ⇒B=2 ⇒T_n =(A/2^n )+2 if T_1 =4, 4=(A/2)+2 ⇒A=4 ⇒T_n =2+(1/2^(n−2) ) Σ_(k=1) ^n T_k =2n+((2(1−(1/2^n )))/(1−(1/2)))=2(n+2)−(1/2^(n−2) )

$${say}\:{T}_{{n}} ={Ap}^{{n}} +{B} \\ $$$${T}_{{n}+\mathrm{1}} ={Ap}^{{n}+\mathrm{1}} +{B} \\ $$$${Ap}^{{n}+\mathrm{1}} +{B}=\mathrm{1}+\frac{{Ap}^{{n}} }{\mathrm{2}}+\frac{{B}}{\mathrm{2}} \\ $$$$\Rightarrow{Ap}^{{n}} \left({p}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{{B}}{\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow{p}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0}\:\Rightarrow{p}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{B}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow{B}=\mathrm{2} \\ $$$$\Rightarrow\boldsymbol{{T}}_{\boldsymbol{{n}}} =\frac{\boldsymbol{{A}}}{\mathrm{2}^{\boldsymbol{{n}}} }+\mathrm{2} \\ $$$${if}\:{T}_{\mathrm{1}} =\mathrm{4}, \\ $$$$\mathrm{4}=\frac{{A}}{\mathrm{2}}+\mathrm{2} \\ $$$$\Rightarrow{A}=\mathrm{4} \\ $$$$\Rightarrow\boldsymbol{{T}}_{\boldsymbol{{n}}} =\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}^{\boldsymbol{{n}}−\mathrm{2}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{T}_{{k}} =\mathrm{2}{n}+\frac{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{2}\left({n}+\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{2}} } \\ $$

Commented by TawaTawa last updated on 10/Dec/19

God bless you sir. I appreciate your time

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$

Commented by TawaTawa last updated on 10/Dec/19

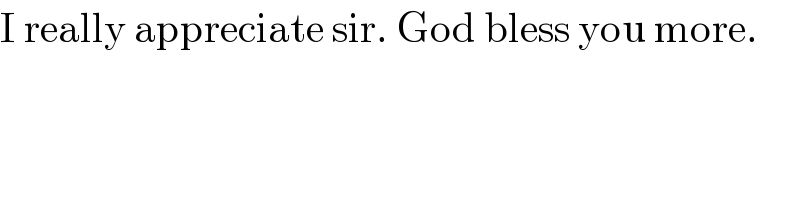
I really appreciate sir. God bless you more.

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}. \\ $$

Commented by TawaTawa last updated on 10/Dec/19

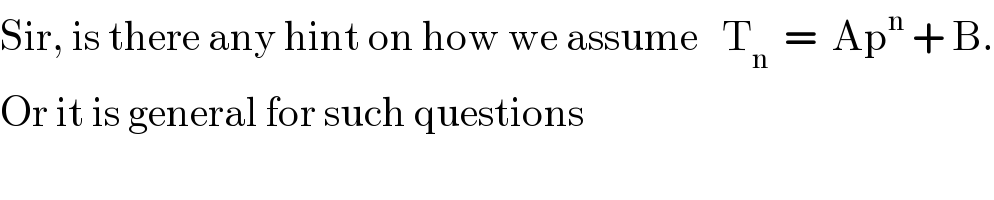
Sir, is there any hint on how we assume T_n = Ap^n + B. Or it is general for such questions

$$\mathrm{Sir},\:\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{hint}\:\mathrm{on}\:\mathrm{how}\:\mathrm{we}\:\mathrm{assume}\:\:\:\mathrm{T}_{\mathrm{n}} \:\:=\:\:\mathrm{Ap}^{\mathrm{n}} \:+\:\mathrm{B}. \\ $$$$\mathrm{Or}\:\mathrm{it}\:\mathrm{is}\:\mathrm{general}\:\mathrm{for}\:\mathrm{such}\:\mathrm{questions} \\ $$

Commented by TawaTawa last updated on 10/Dec/19

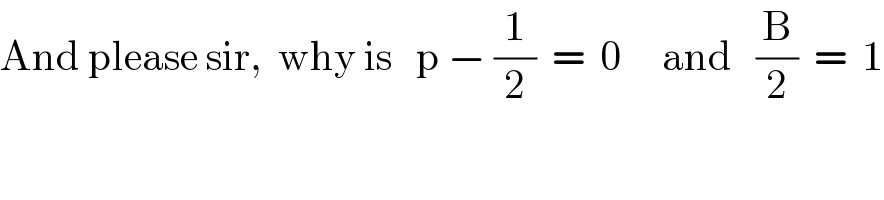
And please sir, why is p − (1/2) = 0 and (B/2) = 1

$$\mathrm{And}\:\mathrm{please}\:\mathrm{sir},\:\:\mathrm{why}\:\mathrm{is}\:\:\:\mathrm{p}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:\:=\:\:\mathrm{0}\:\:\:\:\:\mathrm{and}\:\:\:\frac{\mathrm{B}}{\mathrm{2}}\:\:=\:\:\mathrm{1} \\ $$

Commented by mind is power last updated on 10/Dec/19

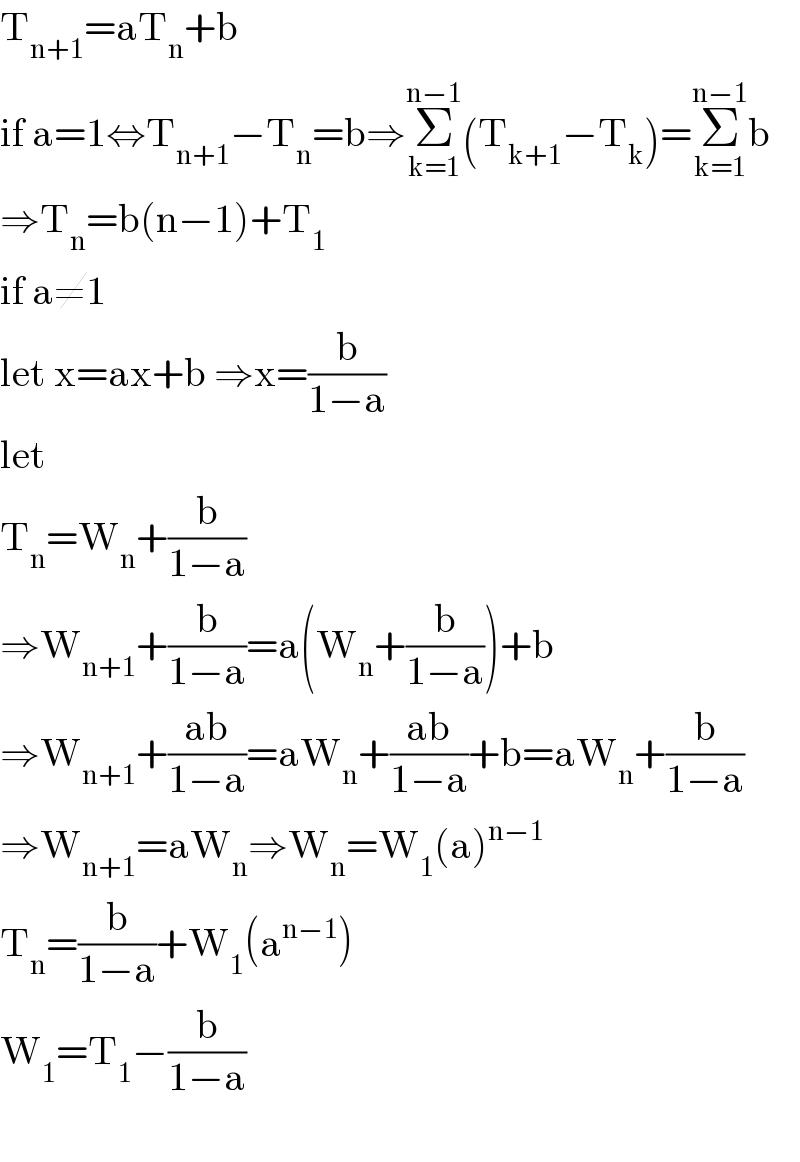
T_(n+1) =aT_n +b if a=1⇔T_(n+1) −T_n =b⇒Σ_(k=1) ^(n−1) (T_(k+1) −T_k )=Σ_(k=1) ^(n−1) b ⇒T_n =b(n−1)+T_1 if a≠1 let x=ax+b ⇒x=(b/(1−a)) let T_n =W_n +(b/(1−a)) ⇒W_(n+1) +(b/(1−a))=a(W_n +(b/(1−a)))+b ⇒W_(n+1) +((ab)/(1−a))=aW_n +((ab)/(1−a))+b=aW_n +(b/(1−a)) ⇒W_(n+1) =aW_n ⇒W_n =W_1 (a)^(n−1) T_n =(b/(1−a))+W_1 (a^(n−1) ) W_1 =T_1 −(b/(1−a))

$$\mathrm{T}_{\mathrm{n}+\mathrm{1}} =\mathrm{aT}_{\mathrm{n}} +\mathrm{b} \\ $$$$\mathrm{if}\:\mathrm{a}=\mathrm{1}\Leftrightarrow\mathrm{T}_{\mathrm{n}+\mathrm{1}} −\mathrm{T}_{\mathrm{n}} =\mathrm{b}\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\left(\mathrm{T}_{\mathrm{k}+\mathrm{1}} −\mathrm{T}_{\mathrm{k}} \right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{b} \\ $$$$\Rightarrow\mathrm{T}_{\mathrm{n}} =\mathrm{b}\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{T}_{\mathrm{1}} \\ $$$$\mathrm{if}\:\mathrm{a}\neq\mathrm{1} \\ $$$$\mathrm{let}\:\mathrm{x}=\mathrm{ax}+\mathrm{b}\:\Rightarrow\mathrm{x}=\frac{\mathrm{b}}{\mathrm{1}−\mathrm{a}} \\ $$$$\mathrm{let}\: \\ $$$$\mathrm{T}_{\mathrm{n}} =\mathrm{W}_{\mathrm{n}} +\frac{\mathrm{b}}{\mathrm{1}−\mathrm{a}} \\ $$$$\Rightarrow\mathrm{W}_{\mathrm{n}+\mathrm{1}} +\frac{\mathrm{b}}{\mathrm{1}−\mathrm{a}}=\mathrm{a}\left(\mathrm{W}_{\mathrm{n}} +\frac{\mathrm{b}}{\mathrm{1}−\mathrm{a}}\right)+\mathrm{b} \\ $$$$\Rightarrow\mathrm{W}_{\mathrm{n}+\mathrm{1}} +\frac{\mathrm{ab}}{\mathrm{1}−\mathrm{a}}=\mathrm{aW}_{\mathrm{n}} +\frac{\mathrm{ab}}{\mathrm{1}−\mathrm{a}}+\mathrm{b}=\mathrm{aW}_{\mathrm{n}} +\frac{\mathrm{b}}{\mathrm{1}−\mathrm{a}} \\ $$$$\Rightarrow\mathrm{W}_{\mathrm{n}+\mathrm{1}} =\mathrm{aW}_{\mathrm{n}} \Rightarrow\mathrm{W}_{\mathrm{n}} =\mathrm{W}_{\mathrm{1}} \left(\mathrm{a}\right)^{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{T}_{\mathrm{n}} =\frac{\mathrm{b}}{\mathrm{1}−\mathrm{a}}+\mathrm{W}_{\mathrm{1}} \left(\mathrm{a}^{\mathrm{n}−\mathrm{1}} \right) \\ $$$$\mathrm{W}_{\mathrm{1}} =\mathrm{T}_{\mathrm{1}} −\frac{\mathrm{b}}{\mathrm{1}−\mathrm{a}} \\ $$$$ \\ $$

Commented by TawaTawa last updated on 10/Dec/19

God bless you sir, thanks for your time

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com