
Question Number 51248 by Tawa1 last updated on 25/Dec/18
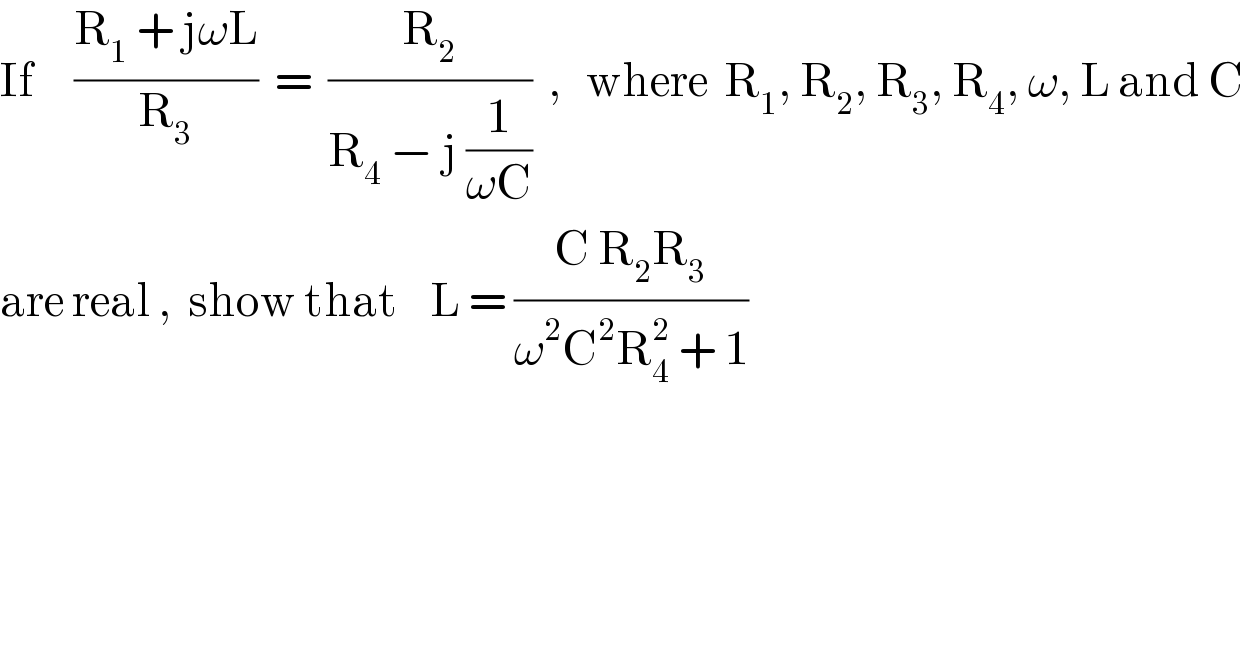
$$\mathrm{If}\:\:\:\:\:\frac{\mathrm{R}_{\mathrm{1}} \:+\:\mathrm{j}\omega\mathrm{L}}{\mathrm{R}_{\mathrm{3}} }\:\:=\:\:\frac{\mathrm{R}_{\mathrm{2}} }{\mathrm{R}_{\mathrm{4}} \:−\:\mathrm{j}\:\frac{\mathrm{1}}{\omega\mathrm{C}}}\:\:,\:\:\:\mathrm{where}\:\:\mathrm{R}_{\mathrm{1}} ,\:\mathrm{R}_{\mathrm{2}} ,\:\mathrm{R}_{\mathrm{3}} ,\:\mathrm{R}_{\mathrm{4}} ,\:\omega,\:\mathrm{L}\:\mathrm{and}\:\mathrm{C} \\ $$$$\mathrm{are}\:\mathrm{real}\:,\:\:\mathrm{show}\:\mathrm{that}\:\:\:\:\mathrm{L}\:=\:\frac{\mathrm{C}\:\mathrm{R}_{\mathrm{2}} \mathrm{R}_{\mathrm{3}} }{\omega^{\mathrm{2}} \mathrm{C}^{\mathrm{2}} \mathrm{R}_{\mathrm{4}} ^{\mathrm{2}} \:+\:\mathrm{1}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Dec/18

$$\frac{{R}_{\mathrm{1}} }{{R}_{\mathrm{3}} }+{j}\frac{{wL}}{{R}_{\mathrm{3}} }=\frac{{R}_{\mathrm{2}} }{{R}_{\mathrm{4}} +\frac{\mathrm{1}}{{w}^{\mathrm{2}} {C}^{\mathrm{2}} }}\left({R}_{\mathrm{4}} +{j}\frac{\mathrm{1}}{{wC}}\right) \\ $$$${comparing}\:{real}\:{and}\:{imaginary}\:{part} \\ $$$$\frac{{wL}}{{R}_{\mathrm{3}} }=\frac{{R}_{\mathrm{2}} }{{R}_{\mathrm{4}} +\frac{\mathrm{1}}{{w}^{\mathrm{2}} {C}^{\mathrm{2}} }}\left(\frac{\mathrm{1}}{{wC}}\right) \\ $$$${L}=\frac{{R}_{\mathrm{3}} }{{w}}×\frac{\frac{{R}_{\mathrm{2}} }{{wC}}}{\frac{{R}_{\mathrm{4}} {w}^{\mathrm{2}} {C}^{\mathrm{2}} +\mathrm{1}}{{w}^{\mathrm{2}} {C}^{\mathrm{2}} }} \\ $$$${L}=\frac{{R}_{\mathrm{3}} }{{w}}×\frac{{R}_{\mathrm{2}} {w}^{\mathrm{2}} {C}^{\mathrm{2}} }{{wC}\left({R}_{\mathrm{4}} {w}^{\mathrm{2}} {C}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{R}_{\mathrm{2}} {R}_{\mathrm{3}} {C}}{\mathrm{1}+{R}_{\mathrm{4}} {w}^{\mathrm{2}} {C}^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by Tawa1 last updated on 25/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

$${thank}\:{you}... \\ $$
