
Question Number 69734 by mhmd last updated on 27/Sep/19
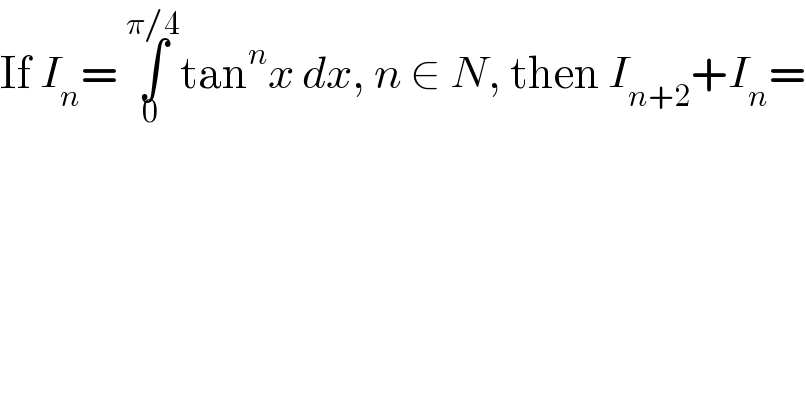
$$\mathrm{If}\:{I}_{{n}} =\:\underset{\mathrm{0}\:} {\overset{\pi/\mathrm{4}} {\int}}\mathrm{tan}^{{n}} {x}\:{dx},\:{n}\:\in\:{N},\:\mathrm{then}\:{I}_{{n}+\mathrm{2}} +{I}_{{n}} = \\ $$
Commented by mathmax by abdo last updated on 16/Oct/19
![I_(n+2) +I_n =∫_0 ^(π/4) (tan^(n+2) x+tan^n x)dx =∫_0 ^(π/4) tan^n x(1+tan^2 x)dx =[(1/(n+1))tan^(n+1) x]_0 ^(π/4) =(1/(n+1))](Q71488.png)
$${I}_{{n}+\mathrm{2}} +{I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left({tan}^{{n}+\mathrm{2}} {x}+{tan}^{{n}} {x}\right){dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tan}^{{n}} {x}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{tan}^{{n}+\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$
