
Question Number 130992 by benjo_mathlover last updated on 31/Jan/21
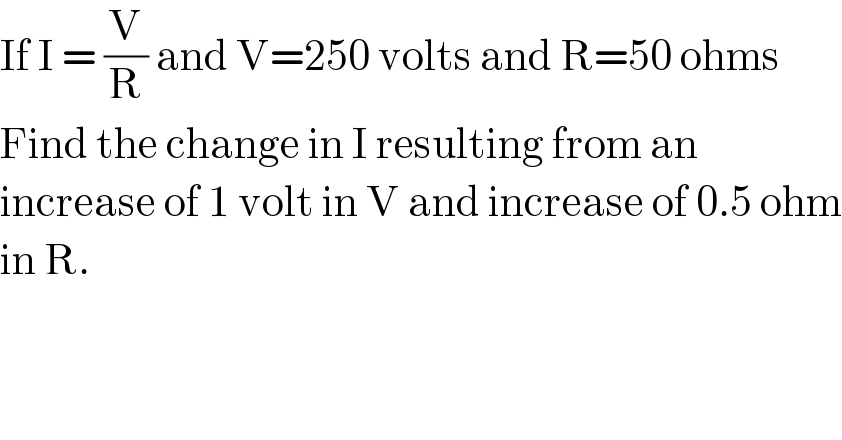
$$\mathrm{If}\:\mathrm{I}\:=\:\frac{\mathrm{V}}{\mathrm{R}}\:\mathrm{and}\:\mathrm{V}=\mathrm{250}\:\mathrm{volts}\:\mathrm{and}\:\mathrm{R}=\mathrm{50}\:\mathrm{ohms} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{change}\:\mathrm{in}\:\mathrm{I}\:\mathrm{resulting}\:\mathrm{from}\:\mathrm{an}\: \\ $$$$\mathrm{increase}\:\mathrm{of}\:\mathrm{1}\:\mathrm{volt}\:\mathrm{in}\:\mathrm{V}\:\mathrm{and}\:\mathrm{increase}\:\mathrm{of}\:\mathrm{0}.\mathrm{5}\:\mathrm{ohm} \\ $$$$\mathrm{in}\:\mathrm{R}. \\ $$
Answered by EDWIN88 last updated on 31/Jan/21
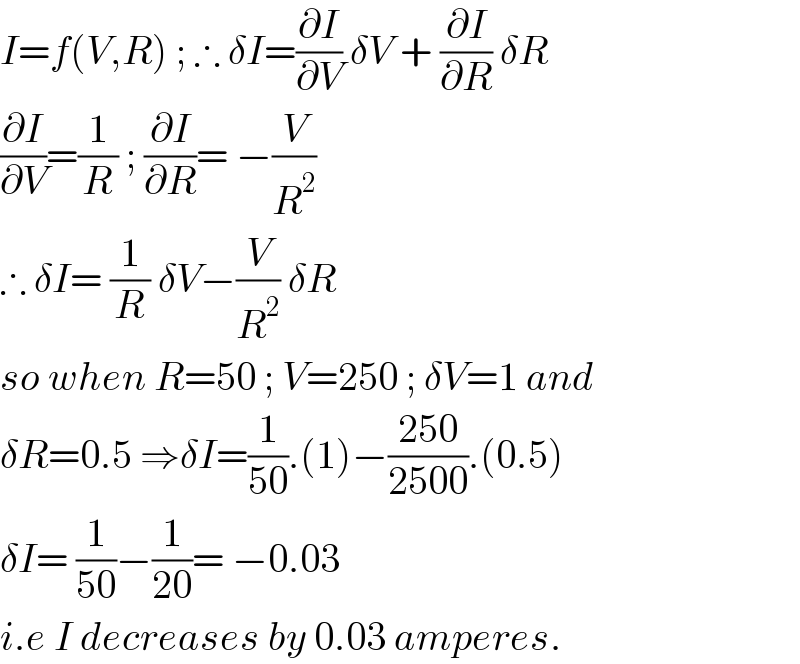
$${I}={f}\left({V},{R}\right)\:;\:\therefore\:\delta{I}=\frac{\partial{I}}{\partial{V}}\:\delta{V}\:+\:\frac{\partial{I}}{\partial{R}}\:\delta{R} \\ $$$$\frac{\partial{I}}{\partial{V}}=\frac{\mathrm{1}}{{R}}\:;\:\frac{\partial{I}}{\partial{R}}=\:−\frac{{V}}{{R}^{\mathrm{2}} }\:\: \\ $$$$\therefore\:\delta{I}=\:\frac{\mathrm{1}}{{R}}\:\delta{V}−\frac{{V}}{{R}^{\mathrm{2}} }\:\delta{R} \\ $$$${so}\:{when}\:{R}=\mathrm{50}\:;\:{V}=\mathrm{250}\:;\:\delta{V}=\mathrm{1}\:{and} \\ $$$$\delta{R}=\mathrm{0}.\mathrm{5}\:\Rightarrow\delta{I}=\frac{\mathrm{1}}{\mathrm{50}}.\left(\mathrm{1}\right)−\frac{\mathrm{250}}{\mathrm{2500}}.\left(\mathrm{0}.\mathrm{5}\right) \\ $$$$\delta{I}=\:\frac{\mathrm{1}}{\mathrm{50}}−\frac{\mathrm{1}}{\mathrm{20}}=\:−\mathrm{0}.\mathrm{03}\: \\ $$$${i}.{e}\:{I}\:{decreases}\:{by}\:\mathrm{0}.\mathrm{03}\:{amperes}. \\ $$
