
Question Number 46465 by rahul 19 last updated on 26/Oct/18
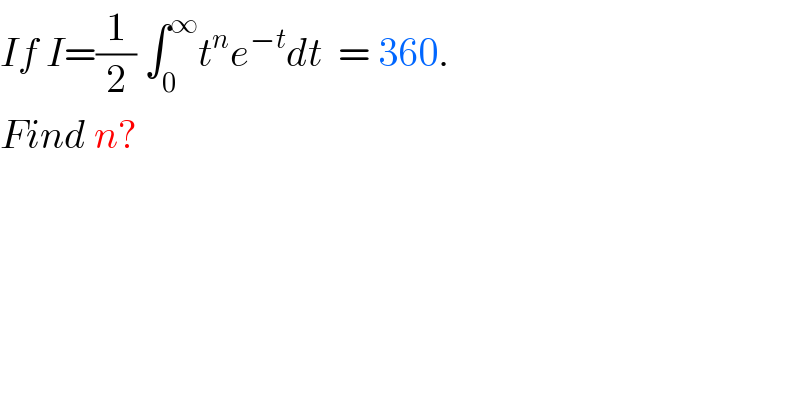
$${If}\:{I}=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} {t}^{{n}} {e}^{−{t}} {dt}\:\:=\:\mathrm{360}. \\ $$$${Find}\:{n}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Oct/18

$${gamma}\:{function} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {t}^{{n}−\mathrm{1}} {dt}=\lceil\left({n}\right) \\ $$$${when}\:\lceil\left({n}+\mathrm{1}\right)={n}\lceil\left({n}\right)={n}! \\ $$$$ \\ $$$${your}\:{problem}\:{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {t}^{{n}+\mathrm{1}−\mathrm{1}} \:{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\lceil\left({n}+\mathrm{1}\right)=\mathrm{360} \\ $$$${n}!=\mathrm{360}×\mathrm{2}=\mathrm{720}=\mathrm{6}! \\ $$$${so}\:{n}=\mathrm{6} \\ $$
Commented by rahul 19 last updated on 27/Oct/18
thanks sir! ����
