
Question Number 218066 by ajfour last updated on 28/Mar/25
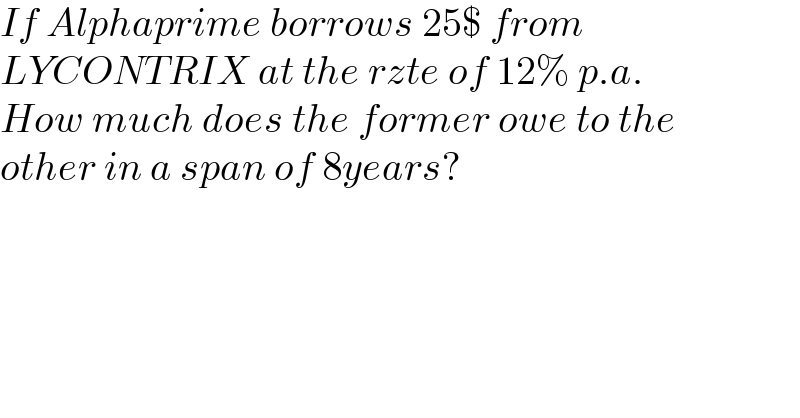
$${If}\:{Alphaprime}\:{borrows}\:\mathrm{25\$}\:{from} \\ $$$${LYCONTRIX}\:{at}\:{the}\:{rzte}\:{of}\:\mathrm{12\%}\:{p}.{a}. \\ $$$${How}\:{much}\:{does}\:{the}\:{former}\:{owe}\:{to}\:{the} \\ $$$${other}\:{in}\:{a}\:{span}\:{of}\:\mathrm{8}{years}? \\ $$
Commented by Frix last updated on 28/Mar/25

$$\mathrm{Strange}\:\mathrm{names}... \\ $$
Commented by ajfour last updated on 01/Apr/25
Ignorance is bliss. btw they are users on this forum
Answered by mr W last updated on 28/Mar/25
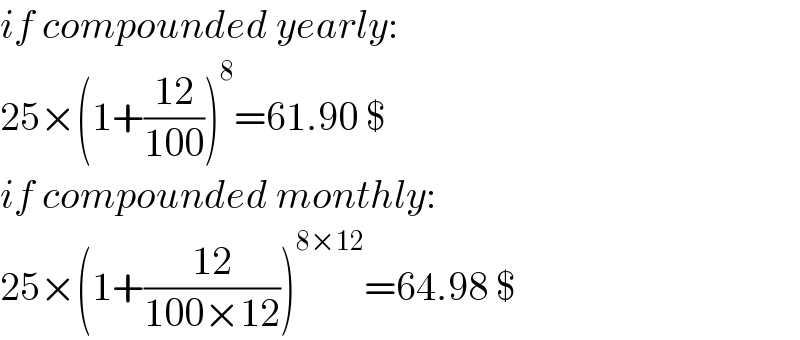
$${if}\:{compounded}\:{yearly}: \\ $$$$\mathrm{25}×\left(\mathrm{1}+\frac{\mathrm{12}}{\mathrm{100}}\right)^{\mathrm{8}} =\mathrm{61}.\mathrm{90}\:\$ \\ $$$${if}\:{compounded}\:{monthly}: \\ $$$$\mathrm{25}×\left(\mathrm{1}+\frac{\mathrm{12}}{\mathrm{100}×\mathrm{12}}\right)^{\mathrm{8}×\mathrm{12}} =\mathrm{64}.\mathrm{98}\:\$ \\ $$
Commented by ajfour last updated on 28/Mar/25
����
Commented by mr W last updated on 29/Mar/25
![lim_(n→∞) 25×(1+((12)/(100×n)))^(8n) =lim_(n→∞) 25×[(1+((12)/(100×n)))^((100×n)/(12)) ]^((8×12)/(100)) =25×e^((8×12)/(100)) =65.23 $](Q218090.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}25}×\left(\mathrm{1}+\frac{\mathrm{12}}{\mathrm{100}×{n}}\right)^{\mathrm{8}{n}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}25}×\left[\left(\mathrm{1}+\frac{\mathrm{12}}{\mathrm{100}×{n}}\right)^{\frac{\mathrm{100}×{n}}{\mathrm{12}}} \right]^{\frac{\mathrm{8}×\mathrm{12}}{\mathrm{100}}} \\ $$$$=\mathrm{25}×{e}^{\frac{\mathrm{8}×\mathrm{12}}{\mathrm{100}}} \\ $$$$=\mathrm{65}.\mathrm{23}\:\$ \\ $$
