Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 41321 by rahul 19 last updated on 05/Aug/18

If A is a square matrix of order 3, then ∣(A−A^T )^(2011) ∣ = ?

$$\mathrm{If}\:\mathrm{A}\:\mathrm{is}\:\mathrm{a}\:\mathrm{square}\:\mathrm{matrix}\:\mathrm{of}\:\mathrm{order}\:\mathrm{3},\:\mathrm{then} \\ $$$$\:\mid\left(\mathrm{A}−\mathrm{A}^{\mathrm{T}} \right)^{\mathrm{2011}} \mid\:=\:? \\ $$

Commented by rahul 19 last updated on 05/Aug/18

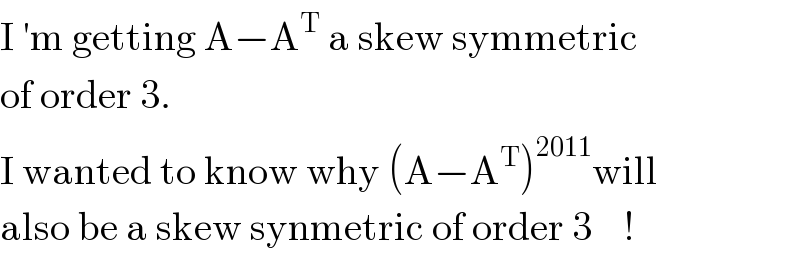
I ′m getting A−A^T a skew symmetric of order 3. I wanted to know why (A−A^T )^(2011) will also be a skew synmetric of order 3 !

$$\mathrm{I}\:'\mathrm{m}\:\mathrm{getting}\:\mathrm{A}−\mathrm{A}^{\mathrm{T}} \:\mathrm{a}\:\mathrm{skew}\:\mathrm{symmetric}\: \\ $$$$\mathrm{of}\:\mathrm{order}\:\mathrm{3}. \\ $$$$\mathrm{I}\:\mathrm{wanted}\:\mathrm{to}\:\mathrm{know}\:\mathrm{why}\:\left(\mathrm{A}−\mathrm{A}^{\mathrm{T}} \right)^{\mathrm{2011}} \mathrm{will} \\ $$$$\mathrm{also}\:\mathrm{be}\:\mathrm{a}\:\mathrm{skew}\:\mathrm{synmetric}\:\mathrm{of}\:\mathrm{order}\:\mathrm{3}\:\:\:\:! \\ $$

Answered by MJS last updated on 05/Aug/18

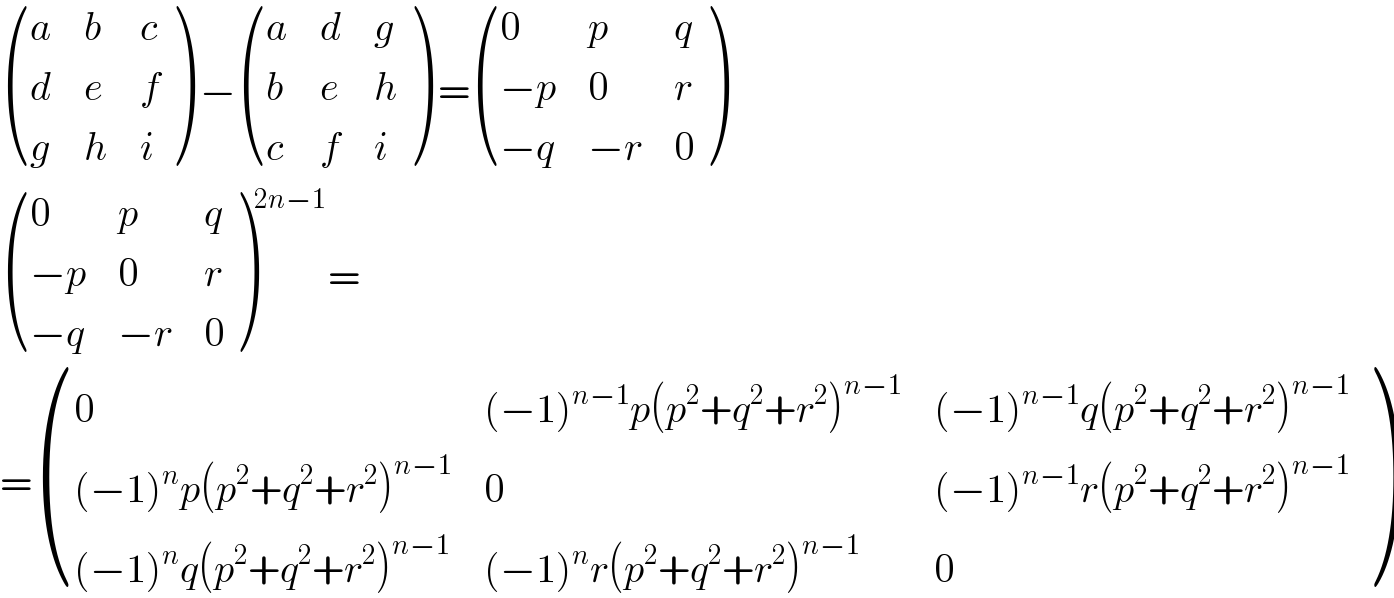
((a,b,c),(d,e,f),(g,h,i) ) − ((a,d,g),(b,e,h),(c,f,i) ) = ((0,p,q),((−p),0,r),((−q),(−r),0) ) ((0,p,q),((−p),0,r),((−q),(−r),0) )^(2n−1) = = ((0,((−1)^(n−1) p(p^2 +q^2 +r^2 )^(n−1) ),((−1)^(n−1) q(p^2 +q^2 +r^2 )^(n−1) )),(((−1)^n p(p^2 +q^2 +r^2 )^(n−1) ),0,((−1)^(n−1) r(p^2 +q^2 +r^2 )^(n−1) )),(((−1)^n q(p^2 +q^2 +r^2 )^(n−1) ),((−1)^n r(p^2 +q^2 +r^2 )^(n−1) ),0) )

$$\begin{pmatrix}{{a}}&{{b}}&{{c}}\\{{d}}&{{e}}&{{f}}\\{{g}}&{{h}}&{{i}}\end{pmatrix}\:−\begin{pmatrix}{{a}}&{{d}}&{{g}}\\{{b}}&{{e}}&{{h}}\\{{c}}&{{f}}&{{i}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{0}}&{{p}}&{{q}}\\{−{p}}&{\mathrm{0}}&{{r}}\\{−{q}}&{−{r}}&{\mathrm{0}}\end{pmatrix} \\ $$$$\begin{pmatrix}{\mathrm{0}}&{{p}}&{{q}}\\{−{p}}&{\mathrm{0}}&{{r}}\\{−{q}}&{−{r}}&{\mathrm{0}}\end{pmatrix}^{\mathrm{2}{n}−\mathrm{1}} = \\ $$$$=\begin{pmatrix}{\mathrm{0}}&{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {p}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} }&{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {q}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} }\\{\left(−\mathrm{1}\right)^{{n}} {p}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} }&{\mathrm{0}}&{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {r}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} }\\{\left(−\mathrm{1}\right)^{{n}} {q}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} }&{\left(−\mathrm{1}\right)^{{n}} {r}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} }&{\mathrm{0}}\end{pmatrix} \\ $$

Commented by rahul 19 last updated on 06/Aug/18

thanks sir ����

Terms of Service

Privacy Policy

Contact: info@tinkutara.com