
Question Number 214050 by CrispyXYZ last updated on 25/Nov/24
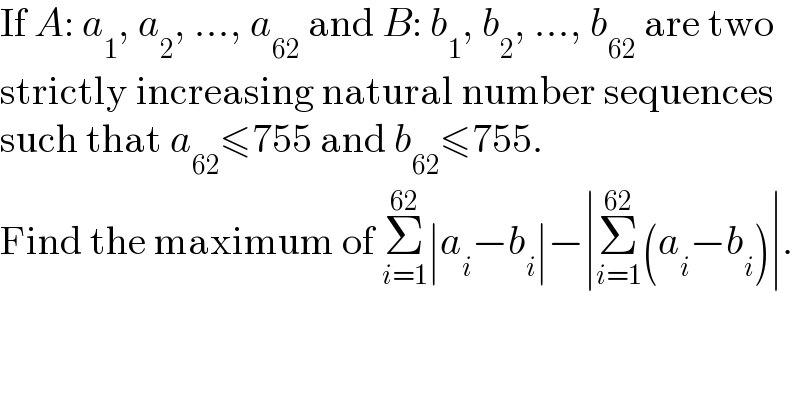
$$\mathrm{If}\:{A}:\:{a}_{\mathrm{1}} ,\:{a}_{\mathrm{2}} ,\:...,\:{a}_{\mathrm{62}} \:\mathrm{and}\:{B}:\:{b}_{\mathrm{1}} ,\:{b}_{\mathrm{2}} ,\:...,\:{b}_{\mathrm{62}} \:\mathrm{are}\:\mathrm{two} \\ $$$$\mathrm{strictly}\:\mathrm{increasing}\:\mathrm{natural}\:\mathrm{number}\:\mathrm{sequences} \\ $$$$\mathrm{such}\:\mathrm{that}\:{a}_{\mathrm{62}} \leqslant\mathrm{755}\:\mathrm{and}\:{b}_{\mathrm{62}} \leqslant\mathrm{755}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{of}\:\underset{{i}=\mathrm{1}} {\overset{\mathrm{62}} {\sum}}\mid{a}_{{i}} −{b}_{{i}} \mid−\mid\underset{{i}=\mathrm{1}} {\overset{\mathrm{62}} {\sum}}\left({a}_{{i}} −{b}_{{i}} \right)\mid. \\ $$
