Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 118435 by bramlexs22 last updated on 17/Oct/20

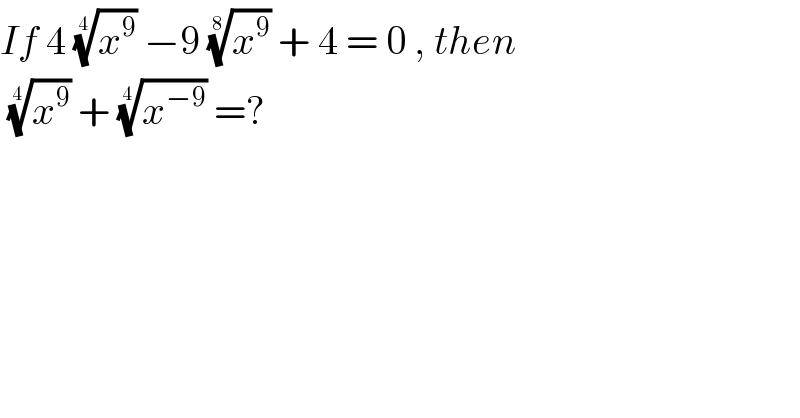
If 4 (x^9 )^(1/(4 )) −9 (x^9 )^(1/(8 )) + 4 = 0 , then (x^9 )^(1/(4 )) + (x^(−9) )^(1/(4 )) =?

$${If}\:\mathrm{4}\:\sqrt[{\mathrm{4}\:}]{{x}^{\mathrm{9}} }\:−\mathrm{9}\:\sqrt[{\mathrm{8}\:}]{{x}^{\mathrm{9}} }\:+\:\mathrm{4}\:=\:\mathrm{0}\:,\:{then}\: \\ $$$$\:\sqrt[{\mathrm{4}\:}]{{x}^{\mathrm{9}} }\:+\:\sqrt[{\mathrm{4}\:}]{{x}^{−\mathrm{9}} }\:=? \\ $$

Answered by benjo_mathlover last updated on 18/Oct/20

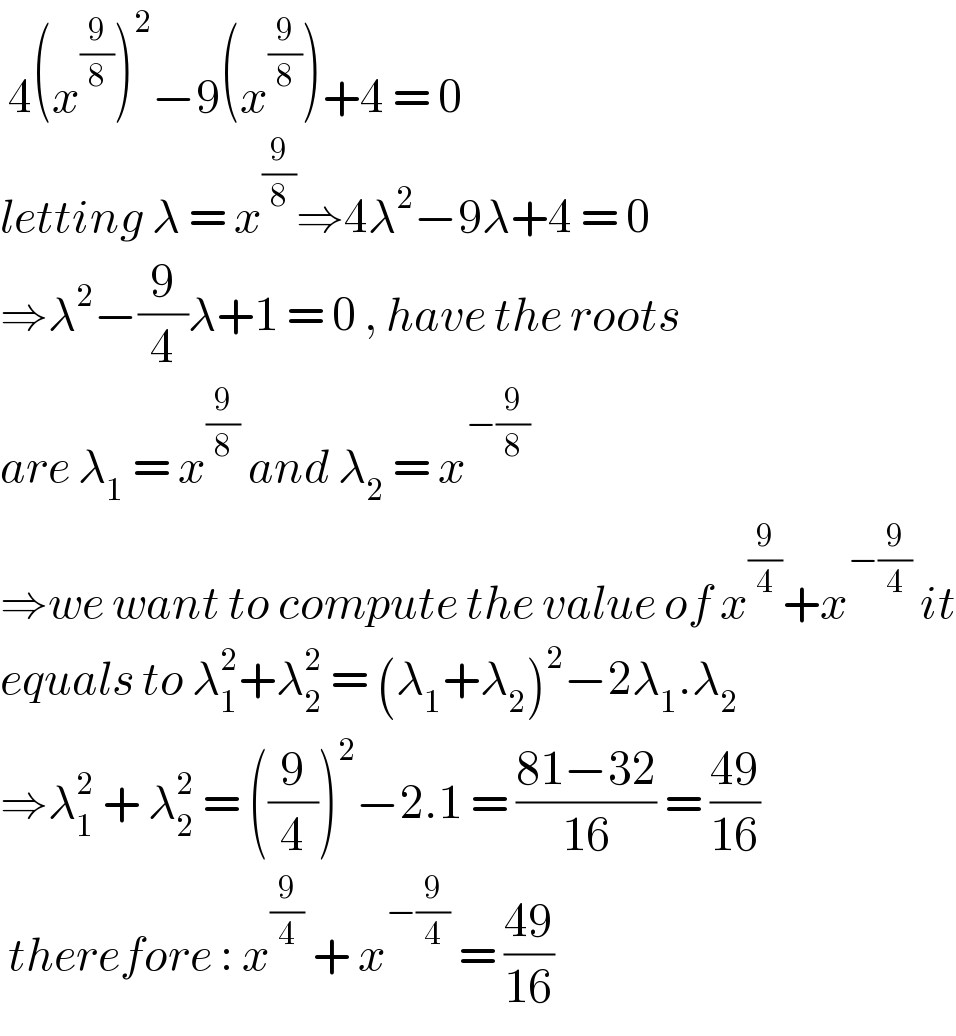
4(x^(9/8) )^2 −9(x^(9/8) )+4 = 0 letting λ = x^(9/8) ⇒4λ^2 −9λ+4 = 0 ⇒λ^2 −(9/4)λ+1 = 0 , have the roots are λ_1 = x^(9/8) and λ_2 = x^(−(9/8)) ⇒we want to compute the value of x^(9/4) +x^(−(9/4)) it equals to λ_1 ^2 +λ_2 ^2 = (λ_1 +λ_2 )^2 −2λ_1 .λ_2 ⇒λ_1 ^2 + λ_2 ^2 = ((9/4))^2 −2.1 = ((81−32)/(16)) = ((49)/(16)) therefore : x^(9/4) + x^(−(9/4)) = ((49)/(16))

$$\:\mathrm{4}\left({x}^{\frac{\mathrm{9}}{\mathrm{8}}} \right)^{\mathrm{2}} −\mathrm{9}\left({x}^{\frac{\mathrm{9}}{\mathrm{8}}} \right)+\mathrm{4}\:=\:\mathrm{0} \\ $$$${letting}\:\lambda\:=\:{x}^{\frac{\mathrm{9}}{\mathrm{8}}} \Rightarrow\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{9}\lambda+\mathrm{4}\:=\:\mathrm{0} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{4}}\lambda+\mathrm{1}\:=\:\mathrm{0}\:,\:{have}\:{the}\:{roots} \\ $$$${are}\:\lambda_{\mathrm{1}} \:=\:{x}^{\frac{\mathrm{9}}{\mathrm{8}}} \:{and}\:\lambda_{\mathrm{2}} \:=\:{x}^{−\frac{\mathrm{9}}{\mathrm{8}}} \\ $$$$\Rightarrow{we}\:{want}\:{to}\:{compute}\:{the}\:{value}\:{of}\:{x}^{\frac{\mathrm{9}}{\mathrm{4}}} +{x}^{−\frac{\mathrm{9}}{\mathrm{4}}} \:{it} \\ $$$${equals}\:{to}\:\lambda_{\mathrm{1}} ^{\mathrm{2}} +\lambda_{\mathrm{2}} ^{\mathrm{2}} \:=\:\left(\lambda_{\mathrm{1}} +\lambda_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\lambda_{\mathrm{1}} .\lambda_{\mathrm{2}} \\ $$$$\Rightarrow\lambda_{\mathrm{1}} ^{\mathrm{2}} \:+\:\lambda_{\mathrm{2}} ^{\mathrm{2}} \:=\:\left(\frac{\mathrm{9}}{\mathrm{4}}\right)^{\mathrm{2}} −\mathrm{2}.\mathrm{1}\:=\:\frac{\mathrm{81}−\mathrm{32}}{\mathrm{16}}\:=\:\frac{\mathrm{49}}{\mathrm{16}} \\ $$$$\:{therefore}\::\:{x}^{\frac{\mathrm{9}}{\mathrm{4}}} \:+\:{x}^{−\frac{\mathrm{9}}{\mathrm{4}}} \:=\:\frac{\mathrm{49}}{\mathrm{16}} \\ $$

Commented by MJS_new last updated on 17/Oct/20

answer is ((49)/(16))

$$\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{49}}{\mathrm{16}} \\ $$

Commented by bramlexs22 last updated on 17/Oct/20

how sir?

$${how}\:{sir}? \\ $$

Commented by MJS_new last updated on 17/Oct/20

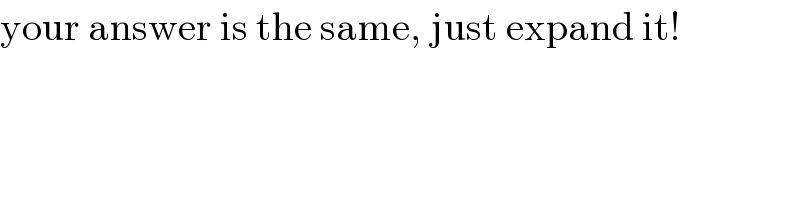
your answer is the same, just expand it!

$$\mathrm{your}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same},\:\mathrm{just}\:\mathrm{expand}\:\mathrm{it}! \\ $$

Answered by MJS_new last updated on 17/Oct/20

we don′t have to solve for x let t=x^(9/8) ⇒ the problem turns to if 4t^2 −9t+4=0 then t^2 +t^(−2) =? 4t^2 −9t+4=0 t^2 −(9/4)t+1=0 the solutions of t^2 +pt+1 are t_1 =((−p−(√(p^2 −4)))/2) and t_2 =t_1 ^(−1) ⇒ t^2 +t^(−2) =t_1 ^2 +t_2 ^2 t_1 ^2 =((p^2 −2+p(√(p^2 −4)))/2)∧t_2 ^2 =((p^2 −2+p(√(p^2 −4)))/2) ⇒ t^2 +t^(−2) =t_1 ^2 +t_2 ^2 =p^2 −2 p=−(9/4) ⇒ answer is ((49)/(16))

$$\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{for}\:{x} \\ $$$$\mathrm{let}\:{t}={x}^{\mathrm{9}/\mathrm{8}} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{problem}\:\mathrm{turns}\:\mathrm{to} \\ $$$$\mathrm{if}\:\mathrm{4}{t}^{\mathrm{2}} −\mathrm{9}{t}+\mathrm{4}=\mathrm{0}\:\mathrm{then}\:{t}^{\mathrm{2}} +{t}^{−\mathrm{2}} =? \\ $$$$\mathrm{4}{t}^{\mathrm{2}} −\mathrm{9}{t}+\mathrm{4}=\mathrm{0} \\ $$$${t}^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{4}}{t}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{solutions}\:\mathrm{of}\:{t}^{\mathrm{2}} +{pt}+\mathrm{1}\:\mathrm{are} \\ $$$${t}_{\mathrm{1}} =\frac{−{p}−\sqrt{{p}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\:\mathrm{and}\:{t}_{\mathrm{2}} ={t}_{\mathrm{1}} ^{−\mathrm{1}} \\ $$$$\Rightarrow\:{t}^{\mathrm{2}} +{t}^{−\mathrm{2}} ={t}_{\mathrm{1}} ^{\mathrm{2}} +{t}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${t}_{\mathrm{1}} ^{\mathrm{2}} =\frac{{p}^{\mathrm{2}} −\mathrm{2}+{p}\sqrt{{p}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\wedge{t}_{\mathrm{2}} ^{\mathrm{2}} =\frac{{p}^{\mathrm{2}} −\mathrm{2}+{p}\sqrt{{p}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{t}^{\mathrm{2}} +{t}^{−\mathrm{2}} ={t}_{\mathrm{1}} ^{\mathrm{2}} +{t}_{\mathrm{2}} ^{\mathrm{2}} ={p}^{\mathrm{2}} −\mathrm{2} \\ $$$${p}=−\frac{\mathrm{9}}{\mathrm{4}}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{49}}{\mathrm{16}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com