Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 101498 by bemath last updated on 03/Jul/20

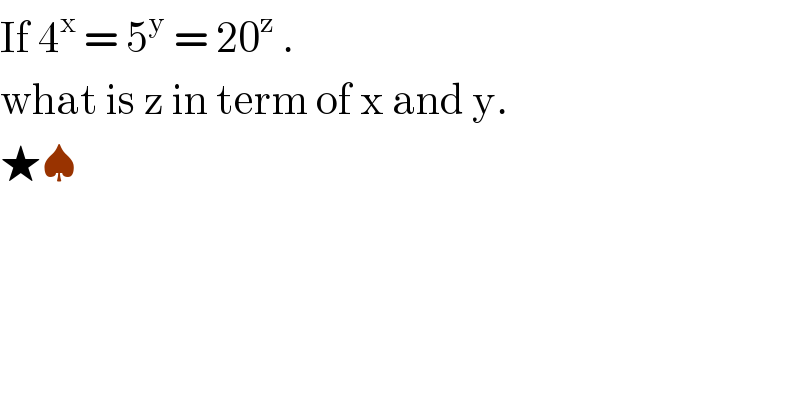
If 4^x = 5^y = 20^z . what is z in term of x and y. ★♠

$$\mathrm{If}\:\mathrm{4}^{\mathrm{x}} \:=\:\mathrm{5}^{\mathrm{y}} \:=\:\mathrm{20}^{\mathrm{z}} \:. \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{z}\:\mathrm{in}\:\mathrm{term}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}. \\ $$$$\bigstar\spadesuit \\ $$

Commented by bobhans last updated on 03/Jul/20

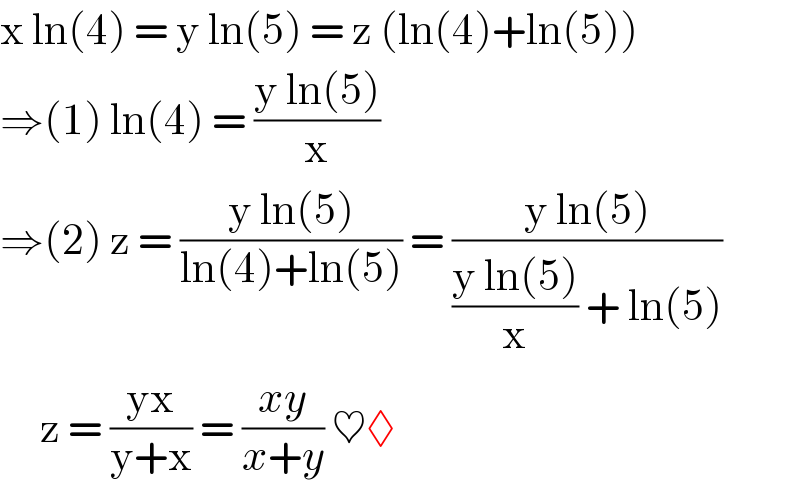
x ln(4) = y ln(5) = z (ln(4)+ln(5)) ⇒(1) ln(4) = ((y ln(5))/x) ⇒(2) z = ((y ln(5))/(ln(4)+ln(5))) = ((y ln(5))/(((y ln(5))/x) + ln(5))) z = ((yx)/(y+x)) = ((xy)/(x+y)) ♥◊

$$\mathrm{x}\:\mathrm{ln}\left(\mathrm{4}\right)\:=\:\mathrm{y}\:\mathrm{ln}\left(\mathrm{5}\right)\:=\:\mathrm{z}\:\left(\mathrm{ln}\left(\mathrm{4}\right)+\mathrm{ln}\left(\mathrm{5}\right)\right) \\ $$$$\Rightarrow\left(\mathrm{1}\right)\:\mathrm{ln}\left(\mathrm{4}\right)\:=\:\frac{\mathrm{y}\:\mathrm{ln}\left(\mathrm{5}\right)}{\mathrm{x}} \\ $$$$\Rightarrow\left(\mathrm{2}\right)\:\mathrm{z}\:=\:\frac{\mathrm{y}\:\mathrm{ln}\left(\mathrm{5}\right)}{\mathrm{ln}\left(\mathrm{4}\right)+\mathrm{ln}\left(\mathrm{5}\right)}\:=\:\frac{\mathrm{y}\:\mathrm{ln}\left(\mathrm{5}\right)}{\frac{\mathrm{y}\:\mathrm{ln}\left(\mathrm{5}\right)}{\mathrm{x}}\:+\:\mathrm{ln}\left(\mathrm{5}\right)} \\ $$$$\:\:\:\:\:\mathrm{z}\:=\:\frac{\mathrm{yx}}{\mathrm{y}+\mathrm{x}}\:=\:\frac{{xy}}{{x}+{y}}\:\heartsuit\lozenge \\ $$

Commented by Dwaipayan Shikari last updated on 03/Jul/20

4^x =5^y =20^z =k (k≠0) 4=k^(1/x) 5=k^(1/y) 20=k^(1/z) k^(1/x) k^(1/y) =k^(1/z) (1/z)=(1/x)+(1/y) ⇒z=((1/x)+(1/y))^(−1) =((xy)/(x+y)) ■ ★ L

$$\mathrm{4}^{{x}} =\mathrm{5}^{{y}} =\mathrm{20}^{{z}} ={k}\:\:\left({k}\neq\mathrm{0}\right) \\ $$$$\mathrm{4}={k}^{\frac{\mathrm{1}}{{x}}} \:\:\:\:\:\mathrm{5}={k}^{\frac{\mathrm{1}}{{y}}} \:\:\:\:\:\mathrm{20}={k}^{\frac{\mathrm{1}}{{z}}} \\ $$$${k}^{\frac{\mathrm{1}}{{x}}} {k}^{\frac{\mathrm{1}}{{y}}} ={k}^{\frac{\mathrm{1}}{{z}}} \\ $$$$\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\:\:\:\:\Rightarrow{z}=\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right)^{−\mathrm{1}} =\frac{{xy}}{{x}+{y}}\:\:\blacksquare\:\bigstar\:\mathscr{L} \\ $$

Commented by bramlex last updated on 03/Jul/20

thank you both

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both}\: \\ $$

Answered by RKT last updated on 03/Jul/20

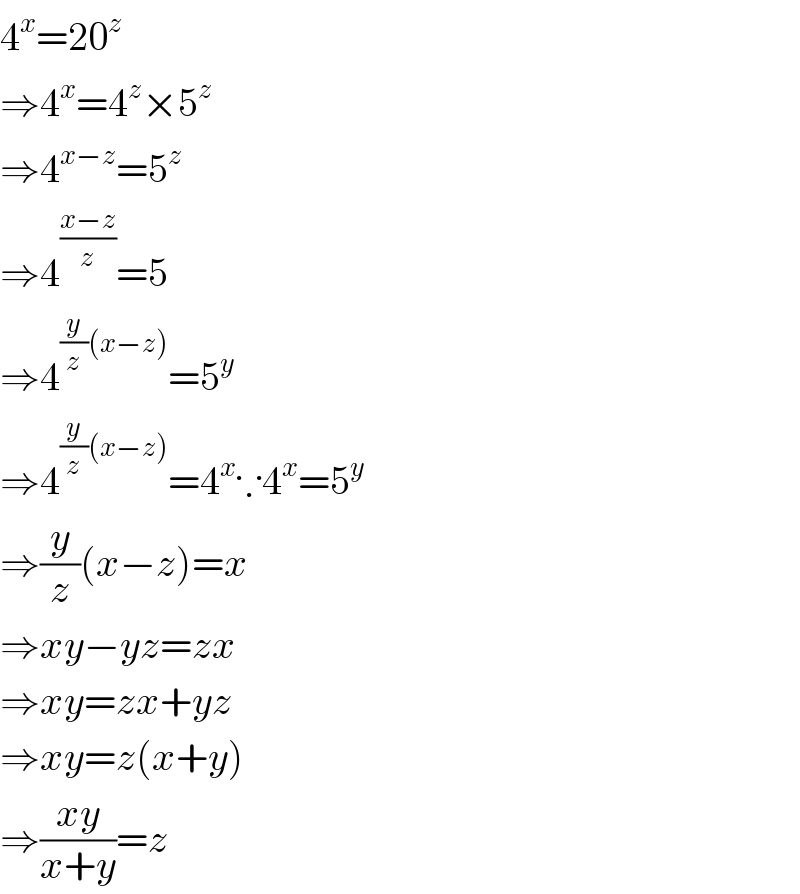
4^x =20^z ⇒4^x =4^z ×5^z ⇒4^(x−z) =5^z ⇒4^((x−z)/z) =5 ⇒4^((y/z)(x−z)) =5^y ⇒4^((y/z)(x−z)) =4^x ∵4^x =5^y ⇒(y/z)(x−z)=x ⇒xy−yz=zx ⇒xy=zx+yz ⇒xy=z(x+y) ⇒((xy)/(x+y))=z

$$\mathrm{4}^{{x}} =\mathrm{20}^{{z}} \\ $$$$\Rightarrow\mathrm{4}^{{x}} =\mathrm{4}^{{z}} ×\mathrm{5}^{{z}} \\ $$$$\Rightarrow\mathrm{4}^{{x}−{z}} =\mathrm{5}^{{z}} \\ $$$$\Rightarrow\mathrm{4}^{\frac{{x}−{z}}{{z}}} =\mathrm{5} \\ $$$$\Rightarrow\mathrm{4}^{\frac{{y}}{{z}}\left({x}−{z}\right)} =\mathrm{5}^{{y}} \\ $$$$\Rightarrow\mathrm{4}^{\frac{{y}}{{z}}\left({x}−{z}\right)} =\mathrm{4}^{{x}} \because\mathrm{4}^{{x}} =\mathrm{5}^{{y}} \\ $$$$\Rightarrow\frac{{y}}{{z}}\left({x}−{z}\right)={x} \\ $$$$\Rightarrow{xy}−{yz}={zx} \\ $$$$\Rightarrow{xy}={zx}+{yz} \\ $$$$\Rightarrow{xy}={z}\left({x}+{y}\right) \\ $$$$\Rightarrow\frac{{xy}}{{x}+{y}}={z} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com