Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 153965 by ZiYangLee last updated on 12/Sep/21

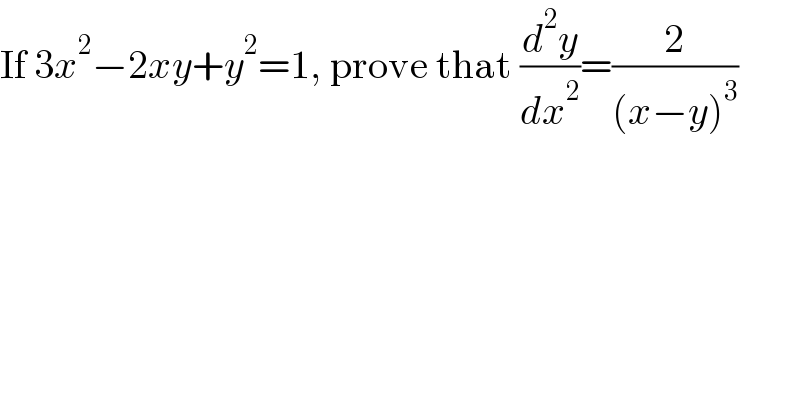
If 3x^2 −2xy+y^2 =1, prove that (d^2 y/dx^2 )=(2/((x−y)^3 ))

$$\mathrm{If}\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{xy}+{y}^{\mathrm{2}} =\mathrm{1},\:\mathrm{prove}\:\mathrm{that}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\mathrm{2}}{\left({x}−{y}\right)^{\mathrm{3}} } \\ $$

Answered by ARUNG_Brandon_MBU last updated on 12/Sep/21

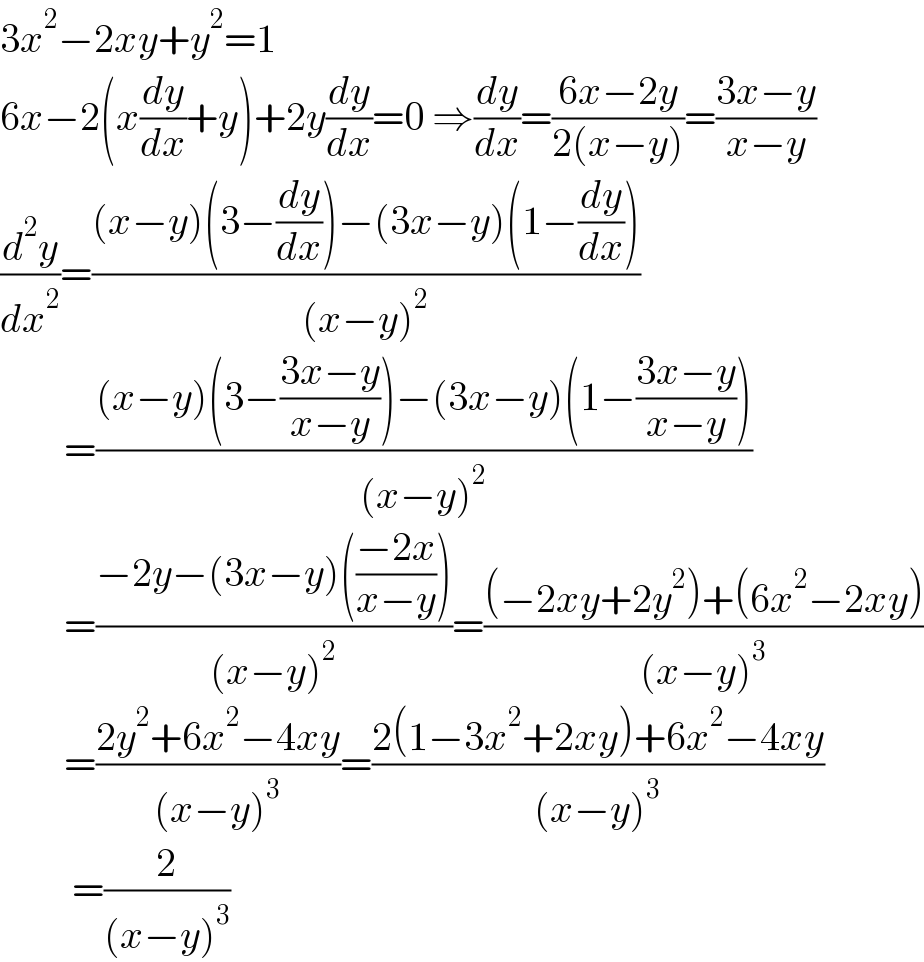
3x^2 −2xy+y^2 =1 6x−2(x(dy/dx)+y)+2y(dy/dx)=0 ⇒(dy/dx)=((6x−2y)/(2(x−y)))=((3x−y)/(x−y)) (d^2 y/dx^2 )=(((x−y)(3−(dy/dx))−(3x−y)(1−(dy/dx)))/((x−y)^2 )) =(((x−y)(3−((3x−y)/(x−y)))−(3x−y)(1−((3x−y)/(x−y))))/((x−y)^2 )) =((−2y−(3x−y)(((−2x)/(x−y))))/((x−y)^2 ))=(((−2xy+2y^2 )+(6x^2 −2xy))/((x−y)^3 )) =((2y^2 +6x^2 −4xy)/((x−y)^3 ))=((2(1−3x^2 +2xy)+6x^2 −4xy)/((x−y)^3 )) =(2/((x−y)^3 ))

$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{xy}+{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{6}{x}−\mathrm{2}\left({x}\frac{{dy}}{{dx}}+{y}\right)+\mathrm{2}{y}\frac{{dy}}{{dx}}=\mathrm{0}\:\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{6}{x}−\mathrm{2}{y}}{\mathrm{2}\left({x}−{y}\right)}=\frac{\mathrm{3}{x}−{y}}{{x}−{y}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\left({x}−{y}\right)\left(\mathrm{3}−\frac{{dy}}{{dx}}\right)−\left(\mathrm{3}{x}−{y}\right)\left(\mathrm{1}−\frac{{dy}}{{dx}}\right)}{\left({x}−{y}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:=\frac{\left({x}−{y}\right)\left(\mathrm{3}−\frac{\mathrm{3}{x}−{y}}{{x}−{y}}\right)−\left(\mathrm{3}{x}−{y}\right)\left(\mathrm{1}−\frac{\mathrm{3}{x}−{y}}{{x}−{y}}\right)}{\left({x}−{y}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:=\frac{−\mathrm{2}{y}−\left(\mathrm{3}{x}−{y}\right)\left(\frac{−\mathrm{2}{x}}{{x}−{y}}\right)}{\left({x}−{y}\right)^{\mathrm{2}} }=\frac{\left(−\mathrm{2}{xy}+\mathrm{2}{y}^{\mathrm{2}} \right)+\left(\mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}{xy}\right)}{\left({x}−{y}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}{xy}}{\left({x}−{y}\right)^{\mathrm{3}} }=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{xy}\right)+\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}{xy}}{\left({x}−{y}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\left({x}−{y}\right)^{\mathrm{3}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com