
Question Number 215640 by BaliramKumar last updated on 12/Jan/25
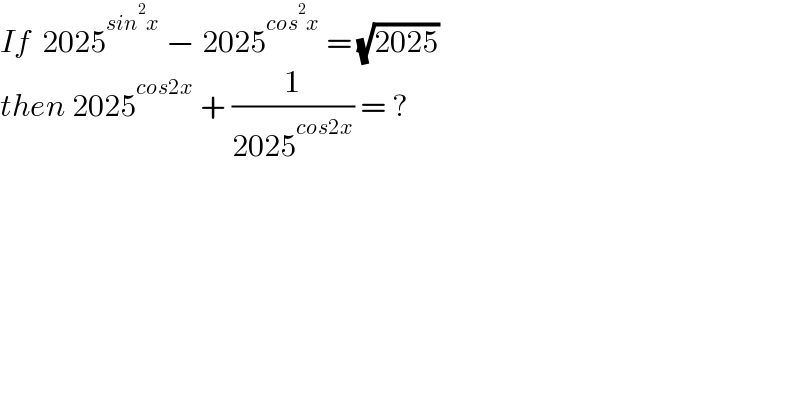
$${If}\:\:\mathrm{2025}^{{sin}^{\mathrm{2}} {x}} \:−\:\mathrm{2025}^{{cos}^{\mathrm{2}} {x}} \:=\:\sqrt{\mathrm{2025}} \\ $$$${then}\:\mathrm{2025}^{{cos}\mathrm{2}{x}} \:+\:\frac{\mathrm{1}}{\mathrm{2025}^{{cos}\mathrm{2}{x}} }\:=\:? \\ $$
Answered by Frix last updated on 13/Jan/25
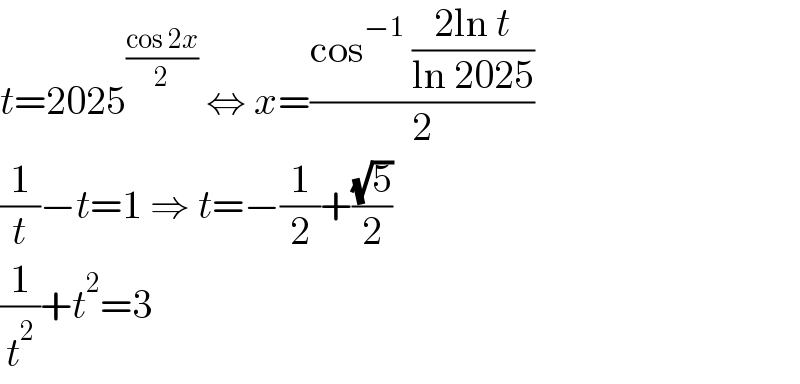
$${t}=\mathrm{2025}^{\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}} \:\Leftrightarrow\:{x}=\frac{\mathrm{cos}^{−\mathrm{1}} \:\frac{\mathrm{2ln}\:{t}}{\mathrm{ln}\:\mathrm{2025}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{t}}−{t}=\mathrm{1}\:\Rightarrow\:{t}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+{t}^{\mathrm{2}} =\mathrm{3} \\ $$
Answered by som(math1967) last updated on 13/Jan/25
![2025^((1−cox2x)/2) −2025^((1+cox2x)/2) =(√(2025)) ⇒(√(2025))[2025^(−((cos2x)/2)) −2025^((cos2x)/2) ]=(√(2025)) ⇒[2025^(−((cos2x)/2)) −2025^((cos2x)/2) ]^2 =1^2 ⇒2025^(−cos2x) +2025^(cox2x) −2.(2025)^0 =1 ∴2025^(cos2x) +(1/(2025^(cos2x) ))=3](Q215648.png)
$$\:\mathrm{2025}^{\frac{\mathrm{1}−{cox}\mathrm{2}{x}}{\mathrm{2}}} −\mathrm{2025}^{\frac{\mathrm{1}+{cox}\mathrm{2}{x}}{\mathrm{2}}} =\sqrt{\mathrm{2025}} \\ $$$$\Rightarrow\sqrt{\mathrm{2025}}\left[\mathrm{2025}^{−\frac{{cos}\mathrm{2}{x}}{\mathrm{2}}} −\mathrm{2025}^{\frac{{cos}\mathrm{2}{x}}{\mathrm{2}}} \right]=\sqrt{\mathrm{2025}} \\ $$$$\Rightarrow\left[\mathrm{2025}^{−\frac{{cos}\mathrm{2}{x}}{\mathrm{2}}} −\mathrm{2025}^{\frac{{cos}\mathrm{2}{x}}{\mathrm{2}}} \right]^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2025}^{−{cos}\mathrm{2}{x}} +\mathrm{2025}^{{cox}\mathrm{2}{x}} −\mathrm{2}.\left(\mathrm{2025}\right)^{\mathrm{0}} \:=\mathrm{1} \\ $$$$\therefore\mathrm{2025}^{{cos}\mathrm{2}{x}} +\frac{\mathrm{1}}{\mathrm{2025}^{{cos}\mathrm{2}{x}} }=\mathrm{3} \\ $$
