
Question Number 137851 by liberty last updated on 07/Apr/21
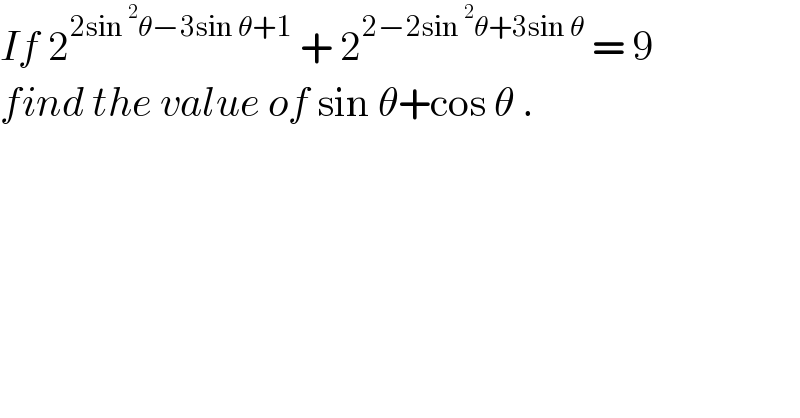
$${If}\:\mathrm{2}^{\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:\theta+\mathrm{1}} \:+\:\mathrm{2}^{\mathrm{2}−\mathrm{2sin}\:^{\mathrm{2}} \theta+\mathrm{3sin}\:\theta} \:=\:\mathrm{9} \\ $$$${find}\:{the}\:{value}\:{of}\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:. \\ $$
Answered by bobhans last updated on 07/Apr/21
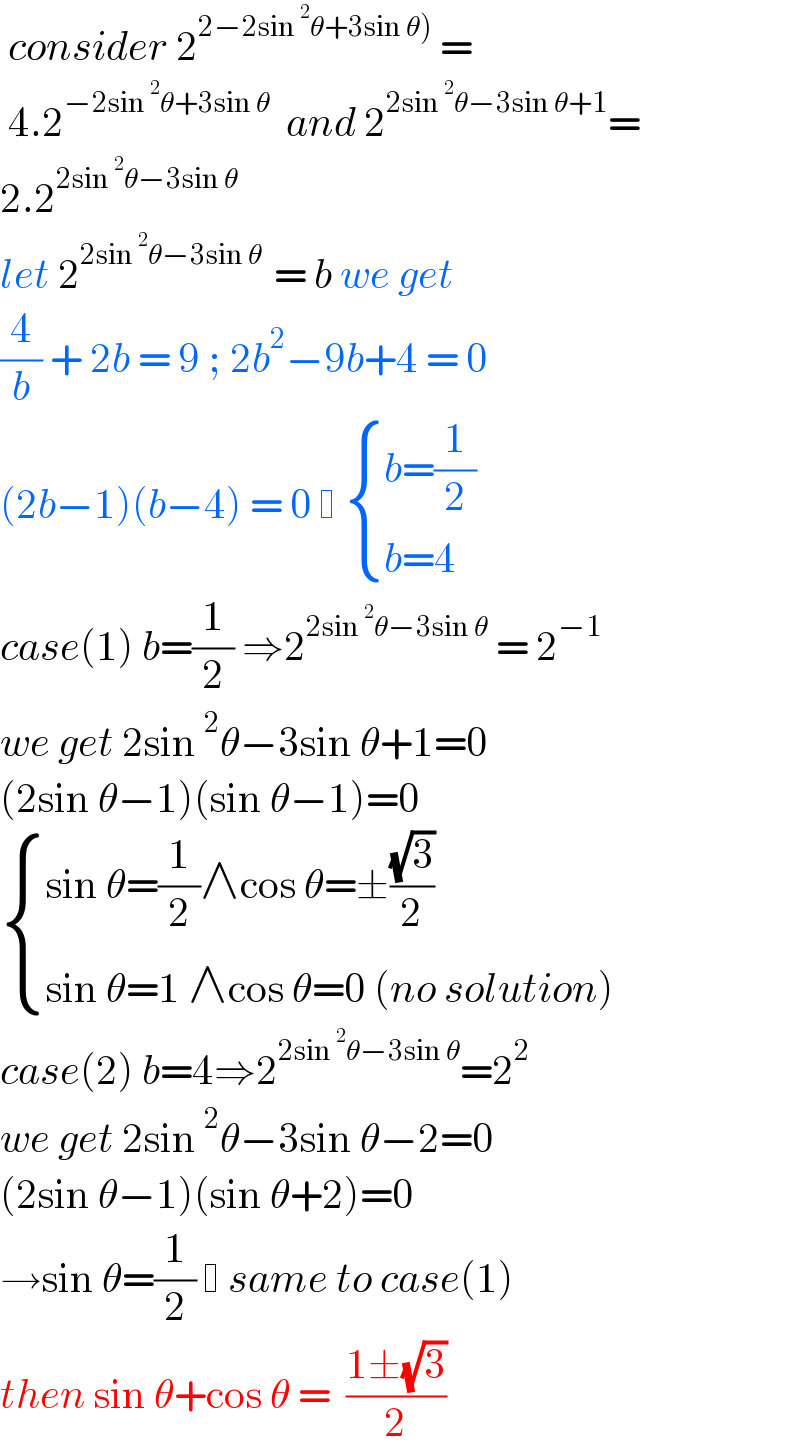
$$\:{consider}\:\mathrm{2}^{\left.\mathrm{2}−\mathrm{2sin}\:^{\mathrm{2}} \theta+\mathrm{3sin}\:\theta\right)} \:=\: \\ $$$$\:\mathrm{4}.\mathrm{2}^{−\mathrm{2sin}\:^{\mathrm{2}} \theta+\mathrm{3sin}\:\theta} \:\:{and}\:\mathrm{2}^{\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:\theta+\mathrm{1}} = \\ $$$$\mathrm{2}.\mathrm{2}^{\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:\theta} \\ $$$${let}\:\mathrm{2}^{\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:\theta\:\:} =\:{b}\:{we}\:{get} \\ $$$$\frac{\mathrm{4}}{{b}}\:+\:\mathrm{2}{b}\:=\:\mathrm{9}\:;\:\mathrm{2}{b}^{\mathrm{2}} −\mathrm{9}{b}+\mathrm{4}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}{b}−\mathrm{1}\right)\left({b}−\mathrm{4}\right)\:=\:\mathrm{0}\: \:\begin{cases}{{b}=\frac{\mathrm{1}}{\mathrm{2}}}\\{{b}=\mathrm{4}}\end{cases} \\ $$$${case}\left(\mathrm{1}\right)\:{b}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{2}^{\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:\theta} \:=\:\mathrm{2}^{−\mathrm{1}} \\ $$$${we}\:{get}\:\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:\theta+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2sin}\:\theta−\mathrm{1}\right)\left(\mathrm{sin}\:\theta−\mathrm{1}\right)=\mathrm{0}\: \\ $$$$\begin{cases}{\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\wedge\mathrm{cos}\:\theta=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:}\\{\mathrm{sin}\:\theta=\mathrm{1}\:\wedge\mathrm{cos}\:\theta=\mathrm{0}\:\left({no}\:{solution}\right)}\end{cases} \\ $$$${case}\left(\mathrm{2}\right)\:{b}=\mathrm{4}\Rightarrow\mathrm{2}^{\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:\theta} =\mathrm{2}^{\mathrm{2}} \\ $$$${we}\:{get}\:\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{3sin}\:\theta−\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{2sin}\:\theta−\mathrm{1}\right)\left(\mathrm{sin}\:\theta+\mathrm{2}\right)=\mathrm{0} \\ $$$$\rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\: \:{same}\:{to}\:{case}\left(\mathrm{1}\right) \\ $$$${then}\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:=\:\:\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
