Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 14002 by Joel577 last updated on 26/May/17

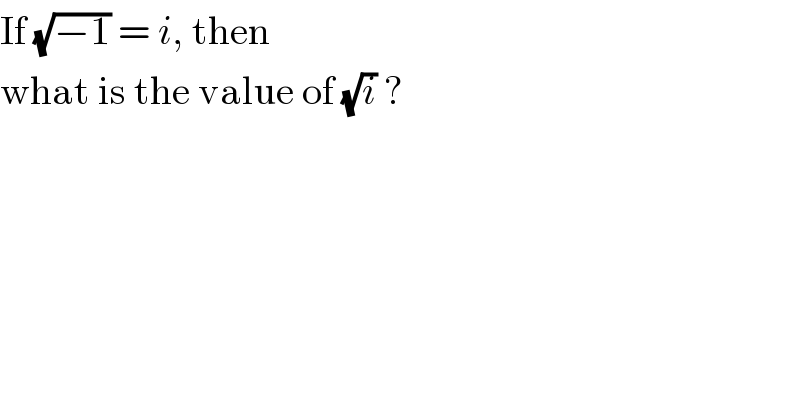
If (√(−1)) = i, then what is the value of (√i) ?

$$\mathrm{If}\:\sqrt{−\mathrm{1}}\:=\:{i},\:\mathrm{then}\: \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\sqrt{{i}}\:? \\ $$

Answered by ajfour last updated on 26/May/17

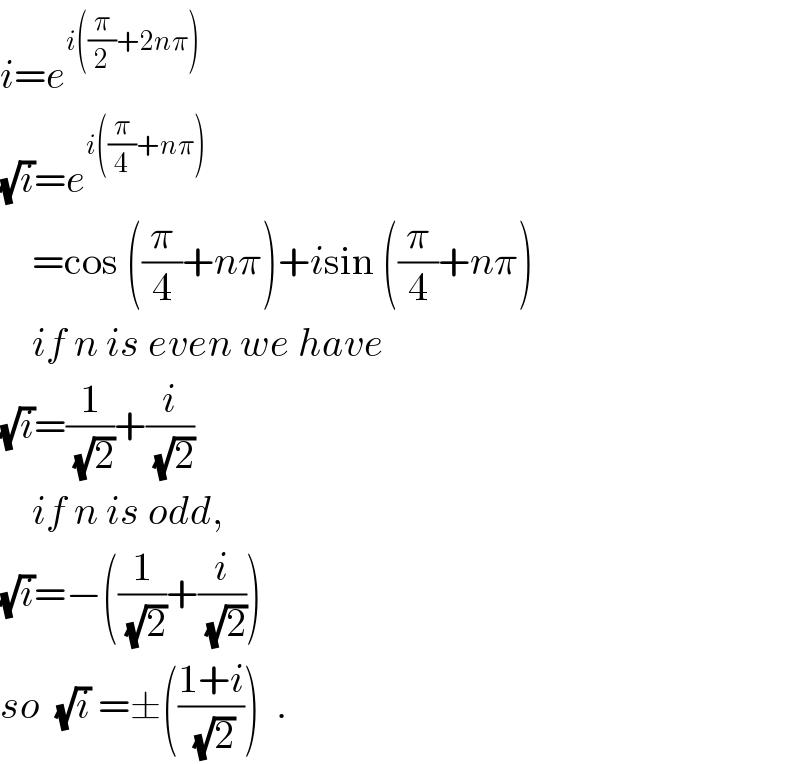
i=e^(i((π/2)+2nπ)) (√i)=e^(i((π/4)+nπ)) =cos ((π/4)+nπ)+isin ((π/4)+nπ) if n is even we have (√i)=(1/(√2))+(i/(√2)) if n is odd, (√i)=−((1/(√2))+(i/(√2))) so (√i) =±(((1+i)/(√2))) .

$${i}={e}^{{i}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{n}\pi\right)} \\ $$$$\sqrt{{i}}={e}^{{i}\left(\frac{\pi}{\mathrm{4}}+{n}\pi\right)} \\ $$$$\:\:\:\:=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}+{n}\pi\right)+{i}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{n}\pi\right) \\ $$$$\:\:\:\:{if}\:{n}\:{is}\:{even}\:{we}\:{have} \\ $$$$\sqrt{{i}}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+\frac{{i}}{\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:{if}\:{n}\:{is}\:{odd}, \\ $$$$\sqrt{{i}}=−\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+\frac{{i}}{\sqrt{\mathrm{2}}}\right)\: \\ $$$${so}\:\:\sqrt{{i}}\:=\pm\left(\frac{\mathrm{1}+{i}}{\sqrt{\mathrm{2}}}\right)\:\:. \\ $$

Commented by tawa tawa last updated on 26/May/17

God bless you sir.....

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.....\: \\ $$

Answered by RasheedSindhi last updated on 26/May/17

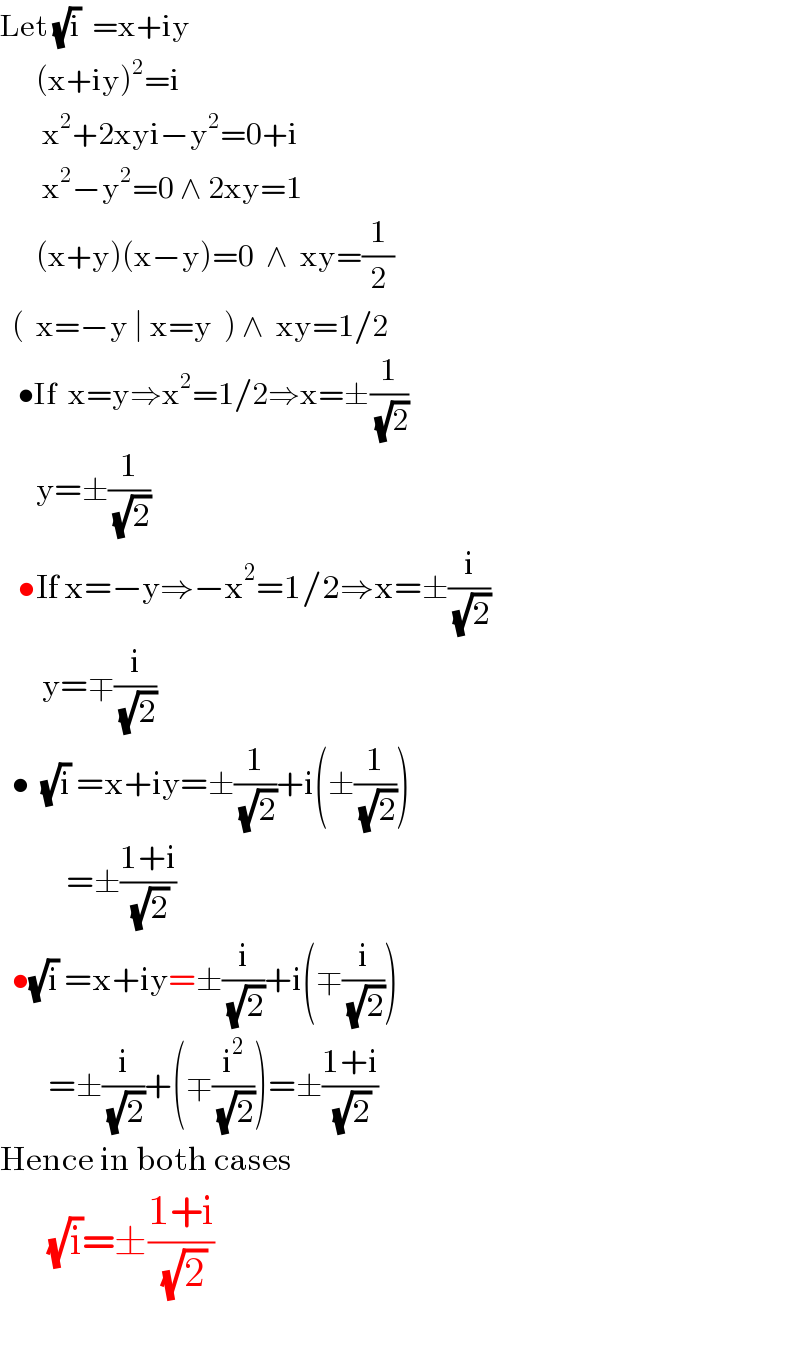
Let (√i) =x+iy (x+iy)^2 =i x^2 +2xyi−y^2 =0+i x^2 −y^2 =0 ∧ 2xy=1 (x+y)(x−y)=0 ∧ xy=(1/2) ( x=−y ∣ x=y ) ∧ xy=1/2 •If x=y⇒x^2 =1/2⇒x=±(1/(√2)) y=±(1/(√2)) •If x=−y⇒−x^2 =1/2⇒x=±(i/(√2)) y=∓(i/(√2)) • (√i) =x+iy=±(1/(√2))+i(±(1/(√2))) =±((1+i)/(√2)) •(√i) =x+iy=±(i/(√2))+i(∓(i/(√2))) =±(i/(√2))+(∓(i^2 /(√2)))=±((1+i)/(√2)) Hence in both cases (√i)=±((1+i)/(√2))

$$\mathrm{Let}\:\sqrt{\mathrm{i}}\:\:=\mathrm{x}+\mathrm{iy} \\ $$$$\:\:\:\:\:\:\left(\mathrm{x}+\mathrm{iy}\right)^{\mathrm{2}} =\mathrm{i} \\ $$$$\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{2xyi}−\mathrm{y}^{\mathrm{2}} =\mathrm{0}+\mathrm{i} \\ $$$$\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} =\mathrm{0}\:\wedge\:\mathrm{2xy}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}−\mathrm{y}\right)=\mathrm{0}\:\:\wedge\:\:\mathrm{xy}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\left(\:\:\mathrm{x}=−\mathrm{y}\:\mid\:\mathrm{x}=\mathrm{y}\:\:\right)\:\wedge\:\:\mathrm{xy}=\mathrm{1}/\mathrm{2} \\ $$$$\:\:\:\bullet\mathrm{If}\:\:\mathrm{x}=\mathrm{y}\Rightarrow\mathrm{x}^{\mathrm{2}} =\mathrm{1}/\mathrm{2}\Rightarrow\mathrm{x}=\pm\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\mathrm{y}=\pm\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\bullet\mathrm{If}\:\mathrm{x}=−\mathrm{y}\Rightarrow−\mathrm{x}^{\mathrm{2}} =\mathrm{1}/\mathrm{2}\Rightarrow\mathrm{x}=\pm\frac{\mathrm{i}}{\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\mathrm{y}=\mp\frac{\mathrm{i}}{\sqrt{\mathrm{2}}} \\ $$$$\:\:\bullet\:\:\sqrt{\mathrm{i}}\:=\mathrm{x}+\mathrm{iy}=\pm\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+\mathrm{i}\left(\pm\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\pm\frac{\mathrm{1}+\mathrm{i}}{\sqrt{\mathrm{2}}} \\ $$$$\:\:\bullet\sqrt{\mathrm{i}}\:=\mathrm{x}+\mathrm{iy}=\pm\frac{\mathrm{i}}{\sqrt{\mathrm{2}}}+\mathrm{i}\left(\mp\frac{\mathrm{i}}{\sqrt{\mathrm{2}}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\pm\frac{\mathrm{i}}{\sqrt{\mathrm{2}}}+\left(\mp\frac{\mathrm{i}^{\mathrm{2}} }{\sqrt{\mathrm{2}}}\right)=\pm\frac{\mathrm{1}+\mathrm{i}}{\sqrt{\mathrm{2}}} \\ $$$$\mathrm{Hence}\:\mathrm{in}\:\mathrm{both}\:\mathrm{cases} \\ $$$$\:\:\:\:\:\:\sqrt{\mathrm{i}}=\pm\frac{\mathrm{1}+\mathrm{i}}{\sqrt{\mathrm{2}}} \\ $$$$ \\ $$

Commented by chux last updated on 26/May/17

wow...... thanks

$$\mathrm{wow}......\:\mathrm{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com