
Question Number 174568 by AgniMath last updated on 04/Aug/22
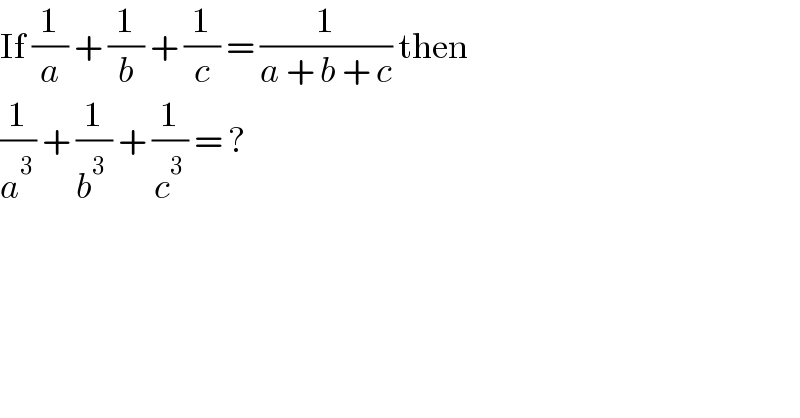
$$\mathrm{If}\:\frac{\mathrm{1}}{{a}}\:+\:\frac{\mathrm{1}}{{b}}\:+\:\frac{\mathrm{1}}{{c}}\:=\:\frac{\mathrm{1}}{{a}\:+\:{b}\:+\:{c}}\:\mathrm{then}\: \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{{b}^{\mathrm{3}} \:}\:+\:\frac{\mathrm{1}}{{c}^{\mathrm{3}} }\:=\:? \\ $$
Answered by behi834171 last updated on 04/Aug/22
![impossible to find. by using: AM-GM iniquality: [((Σx_i )/3)≥((Πx_i ))^(1/3) ] ⇒Σ(1/a)≥3((Π(1/a)))^(1/3) ⇒^((Σ(1/a)=(1/(Σa)))) (1/(Σa))≥3((Π(1/a)))^(1/3) ⇒ ⇒Σa≤(1/(3((Π(1/a)))^(1/3) ))=(1/3).((Πa))^(1/3) and we know that:[AM−GM inq.] Σa≥3((Πa))^(1/3) i.e: 3((Πa))^(1/3) ≤Σa≤(1/3).((Πa))^(1/3) and this is impossible.](Q174580.png)
$$\boldsymbol{{impossible}}\:\boldsymbol{{to}}\:\boldsymbol{{find}}. \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{using}}:\:\boldsymbol{{AM}}-\boldsymbol{{GM}}\:\boldsymbol{{iniquality}}: \\ $$$$\left[\frac{\Sigma\boldsymbol{{x}}_{\boldsymbol{{i}}} }{\mathrm{3}}\geqslant\sqrt[{\mathrm{3}}]{\Pi\boldsymbol{{x}}_{\boldsymbol{{i}}} }\right] \\ $$$$\Rightarrow\Sigma\frac{\mathrm{1}}{\boldsymbol{{a}}}\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\Pi\frac{\mathrm{1}}{\boldsymbol{{a}}}}\:\:\overset{\left(\Sigma\frac{\mathrm{1}}{\boldsymbol{{a}}}=\frac{\mathrm{1}}{\Sigma\boldsymbol{{a}}}\right)} {\Rightarrow}\:\frac{\mathrm{1}}{\Sigma\boldsymbol{{a}}}\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\Pi\frac{\mathrm{1}}{\boldsymbol{{a}}}}\Rightarrow \\ $$$$\Rightarrow\Sigma\boldsymbol{{a}}\leqslant\frac{\mathrm{1}}{\mathrm{3}\sqrt[{\mathrm{3}}]{\Pi\frac{\mathrm{1}}{\boldsymbol{{a}}}}}=\frac{\mathrm{1}}{\mathrm{3}}.\sqrt[{\mathrm{3}}]{\Pi\boldsymbol{{a}}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{we}}\:\boldsymbol{{know}}\:\boldsymbol{{that}}:\left[\boldsymbol{{AM}}−\boldsymbol{{GM}}\:\boldsymbol{{inq}}.\right] \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Sigma\boldsymbol{{a}}\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\Pi\boldsymbol{{a}}}\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\boldsymbol{{i}}.\boldsymbol{{e}}:\:\:\:\:\mathrm{3}\sqrt[{\mathrm{3}}]{\Pi\boldsymbol{{a}}}\leqslant\Sigma\boldsymbol{{a}}\leqslant\frac{\mathrm{1}}{\mathrm{3}}.\sqrt[{\mathrm{3}}]{\Pi\boldsymbol{{a}}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{impossible}}. \\ $$
