
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 171441 by alcohol last updated on 15/Jun/22
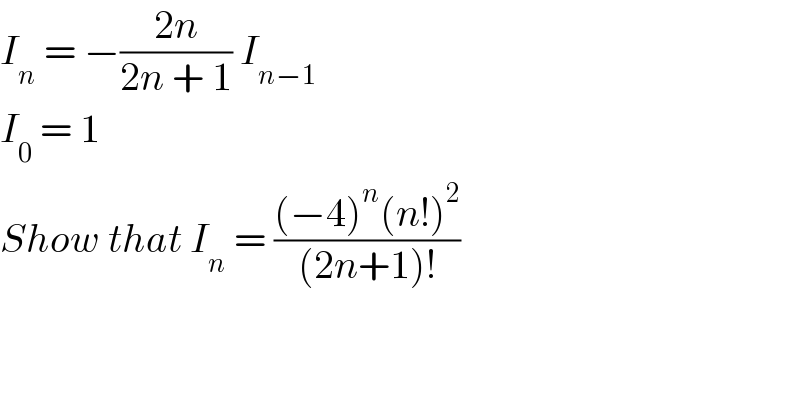
$${I}_{{n}} \:=\:−\frac{\mathrm{2}{n}}{\mathrm{2}{n}\:+\:\mathrm{1}}\:{I}_{{n}−\mathrm{1}} \\ $$$${I}_{\mathrm{0}} \:=\:\mathrm{1} \\ $$$${Show}\:{that}\:{I}_{{n}} \:=\:\frac{\left(−\mathrm{4}\right)^{{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$
Commented by infinityaction last updated on 15/Jun/22
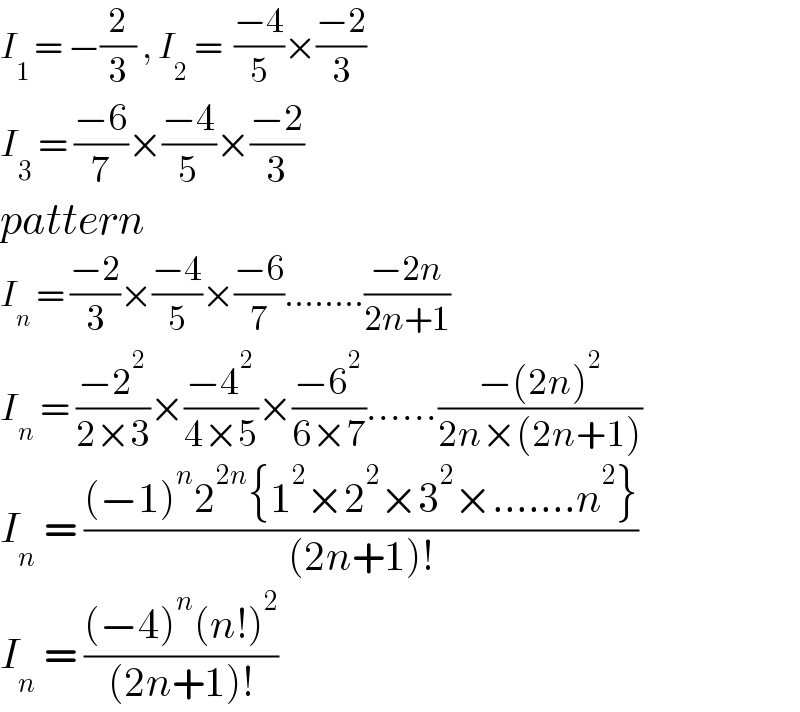
$${I}_{\mathrm{1}\:} =\:−\frac{\mathrm{2}}{\mathrm{3}}\:,\:{I}_{\mathrm{2}} \:=\:\:\frac{−\mathrm{4}}{\mathrm{5}}×\frac{−\mathrm{2}}{\mathrm{3}} \\ $$$${I}_{\mathrm{3}} \:=\:\frac{−\mathrm{6}}{\mathrm{7}}×\frac{−\mathrm{4}}{\mathrm{5}}×\frac{−\mathrm{2}}{\mathrm{3}} \\ $$$${pattern} \\ $$$${I}_{{n}} \:=\:\frac{−\mathrm{2}}{\mathrm{3}}×\frac{−\mathrm{4}}{\mathrm{5}}×\frac{−\mathrm{6}}{\mathrm{7}}........\frac{−\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$${I}_{{n}} \:=\:\frac{−\mathrm{2}^{\mathrm{2}} }{\mathrm{2}×\mathrm{3}}×\frac{−\mathrm{4}^{\mathrm{2}} }{\mathrm{4}×\mathrm{5}}×\frac{−\mathrm{6}^{\mathrm{2}} }{\mathrm{6}×\mathrm{7}}......\frac{−\left(\mathrm{2}{n}\right)^{\mathrm{2}} }{\mathrm{2}{n}×\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$${I}_{{n}} \:=\:\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{2}^{\mathrm{2}{n}} \left\{\mathrm{1}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{2}} ×.......{n}^{\mathrm{2}} \right\}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$${I}_{{n}} \:=\:\frac{\left(−\mathrm{4}\right)^{{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$
