
Question Number 171039 by Kodjo last updated on 06/Jun/22
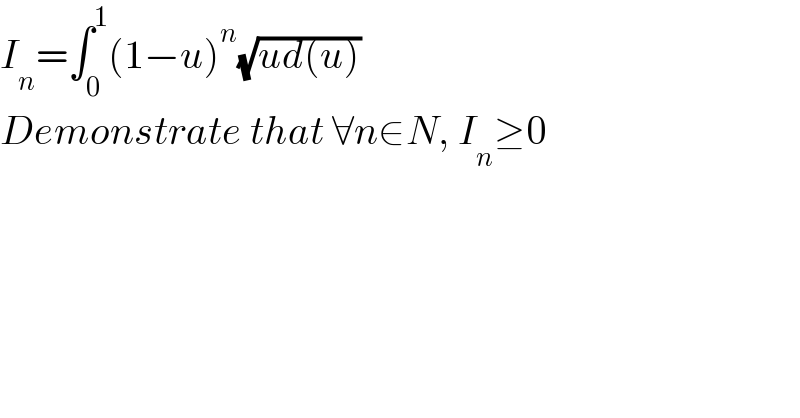
$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} \sqrt{{ud}\left({u}\right)} \\ $$$${Demonstrate}\:{that}\:\forall{n}\in{N},\:{I}_{{n}} \geq\mathrm{0} \\ $$
Answered by thfchristopher last updated on 07/Jun/22
![I_n =∫_0 ^1 (√u)(1−u)^n du =∫_0 ^1 (√u)(1−u)(1−u)^(n−1) du =∫_0 ^1 (√u)(1−u)^(n−1) du−∫_0 ^1 u^(3/2) (1−u)^(n−1) du =I_(n−1) +(1/n)∫_0 ^1 u^(3/2) d[(1−u)^n ] =I_(n−1) +[(1/n)u^(3/2) (1−u)^n ]_0 ^1 −(1/n)∫_0 ^1 (1−u)^n d(u^(3/2) ) =I_(n−1) −(3/(2n))∫_0 ^1 (√u)(1−u)^n du =I_(n−1) −(3/(2n))I_n ∴ (1+(3/(2n)))I_n =I_(n−1) ⇒I_n =((2n)/(2n+3))I_(n−1) =(((2n)(2n−2)...(2))/((2n+3)(2n+1)...(5)))I_0 I_0 =∫_0 ^1 (√u)du =(2/3)[u^(3/2) ]_0 ^1 =(2/3) ∴ I_n =(((2n)(2n−2)...(2)^2 )/((2n+3)(2n+1)...(5)(3)))](Q171059.png)
$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{u}}\left(\mathrm{1}−{u}\right)^{{n}} {du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{u}}\left(\mathrm{1}−{u}\right)\left(\mathrm{1}−{u}\right)^{{n}−\mathrm{1}} {du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{u}}\left(\mathrm{1}−{u}\right)^{{n}−\mathrm{1}} {du}−\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}−{u}\right)^{{n}−\mathrm{1}} {du} \\ $$$$={I}_{{n}−\mathrm{1}} +\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\frac{\mathrm{3}}{\mathrm{2}}} {d}\left[\left(\mathrm{1}−{u}\right)^{{n}} \right] \\ $$$$={I}_{{n}−\mathrm{1}} +\left[\frac{\mathrm{1}}{{n}}{u}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}−{u}\right)^{{n}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} {d}\left({u}^{\frac{\mathrm{3}}{\mathrm{2}}} \right) \\ $$$$={I}_{{n}−\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{2}{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{u}}\left(\mathrm{1}−{u}\right)^{{n}} {du} \\ $$$$={I}_{{n}−\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{2}{n}}{I}_{{n}} \\ $$$$\therefore\:\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}{n}}\right){I}_{{n}} ={I}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{3}}{I}_{{n}−\mathrm{1}} \\ $$$$=\frac{\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}−\mathrm{2}\right)...\left(\mathrm{2}\right)}{\left(\mathrm{2}{n}+\mathrm{3}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)...\left(\mathrm{5}\right)}{I}_{\mathrm{0}} \\ $$$${I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{u}}{du} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left[{u}^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\therefore\:{I}_{{n}} =\frac{\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}−\mathrm{2}\right)...\left(\mathrm{2}\overset{\mathrm{2}} {\right)}}{\left(\mathrm{2}{n}+\mathrm{3}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)...\left(\mathrm{5}\right)\left(\mathrm{3}\right)} \\ $$$$ \\ $$
Commented by Kodjo last updated on 07/Jun/22
thanks
