
Question Number 177134 by DAVONG last updated on 01/Oct/22
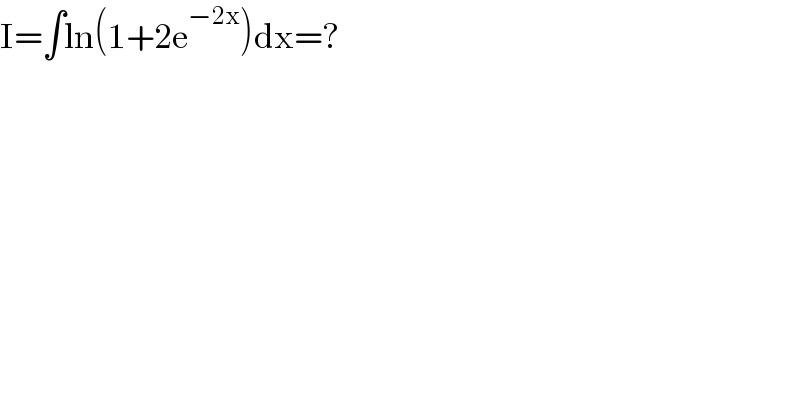
$$\mathrm{I}=\int\mathrm{ln}\left(\mathrm{1}+\mathrm{2e}^{−\mathrm{2x}} \right)\mathrm{dx}=? \\ $$
Answered by Frix last updated on 02/Oct/22
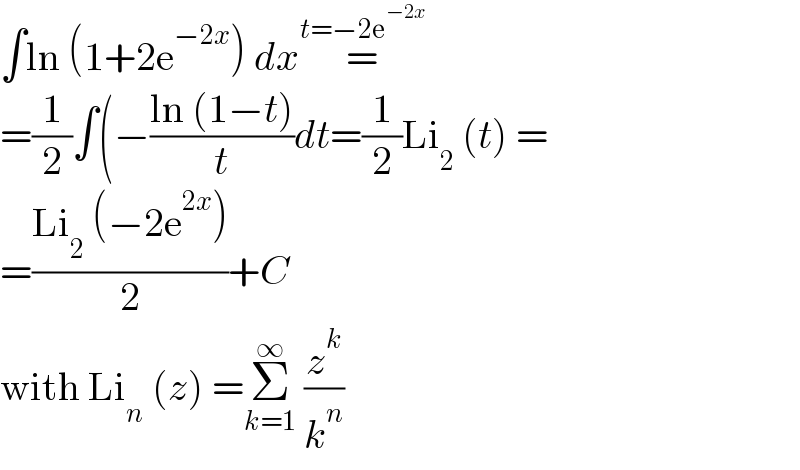
$$\int\mathrm{ln}\:\left(\mathrm{1}+\mathrm{2e}^{−\mathrm{2}{x}} \right)\:{dx}\overset{{t}=−\mathrm{2e}^{−\mathrm{2}{x}} } {=} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(−\frac{\mathrm{ln}\:\left(\mathrm{1}−{t}\right)}{{t}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \:\left({t}\right)\:=\right. \\ $$$$=\frac{\mathrm{Li}_{\mathrm{2}} \:\left(−\mathrm{2e}^{\mathrm{2}{x}} \right)}{\mathrm{2}}+{C} \\ $$$$\mathrm{with}\:\mathrm{Li}_{{n}} \:\left({z}\right)\:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{z}^{{k}} }{{k}^{{n}} } \\ $$
