
Question Number 217148 by Marzuk last updated on 03/Mar/25

$${I}\:{have}\:{seen}\:{a}\:{relationship}\:{in}\:{the}\:{curve} \\ $$$${path}\:{of}\:{a}\:{thrown}\:{object}\:{at}\:\beta\: \\ $$$${while}\:{the}\:{total}\:{passed}\:{distance}\:{D}_{{v}} \:{and} \\ $$$${highest}\:{point}\:{had}\:{passedD}_{{u}} \\ $$$${then}\:\beta\:=\:{arctan}\left(\frac{\mathrm{4}{D}_{{u}} }{{D}_{{v}} }\right) \\ $$$${but}\:{cant}\:{find}\:{the}\:{proof}. \\ $$$${I}\:{would}\:{like}\:{to}\:{say}\:{would}\:{anyone}\:{like} \\ $$$${to}\:{proove}\:{it}?{then}\:{please}. \\ $$
Answered by mr W last updated on 03/Mar/25
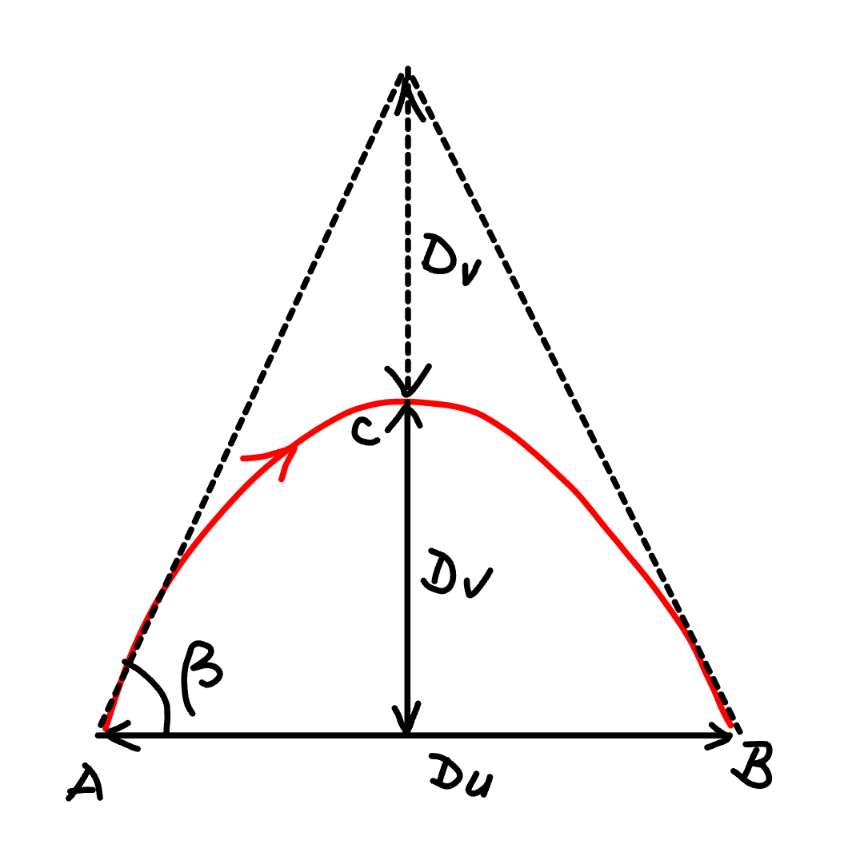
Commented by mr W last updated on 03/Mar/25

$${the}\:{track}\:{of}\:{a}\:{thrown}\:{object}\:{is}\:{a} \\ $$$${parabola}\:\left({red}\:{curce}\:{in}\:{diagram}\right). \\ $$$${for}\:{a}\:{parabola}\:{there}\:{are}\:{the}\: \\ $$$${geometrical}\:{relationships}\:{as}\:{shown}. \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{2}{D}_{{v}} }{\mathrm{0}.\mathrm{5}\:{D}_{{u}} }=\frac{\mathrm{4}{D}_{{v}} }{{D}_{{u}} } \\ $$$$\Rightarrow\beta={arctan}\:\left(\frac{\mathrm{4}{D}_{{v}} }{{D}_{{u}} }\right) \\ $$$${certainly}\:{we}\:{can}\:{also}\:{prove}\:{this} \\ $$$${using}\:{the}\:{equations}\:{for}\:{projectile} \\ $$$${motion},\:{see}\:{below}. \\ $$
Answered by mr W last updated on 03/Mar/25
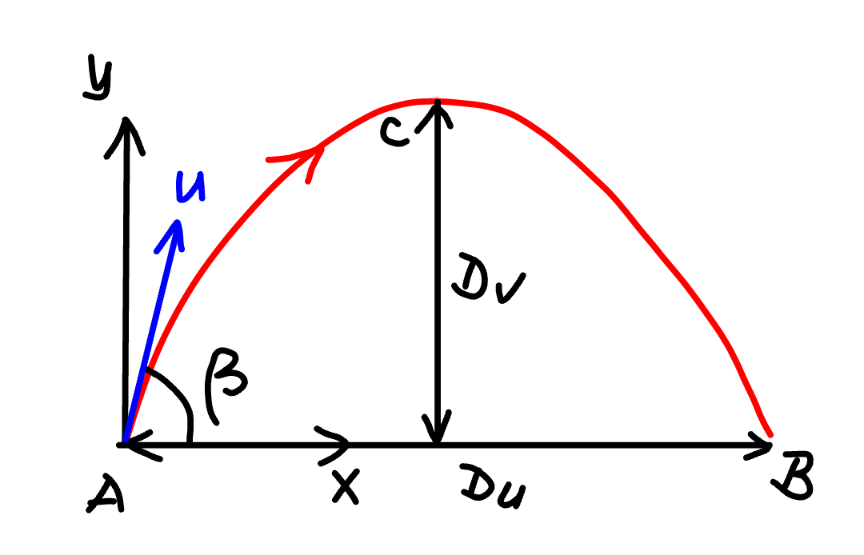
Commented by Marzuk last updated on 03/Mar/25

$${Much}\:{appreciated}!{It}\:{might}\:{need}\:{some} \\ $$$${more}\:{expansion}\:{to}\:{publish}\:{it}.{I}\:{will} \\ $$$${do}\:{it}. \\ $$$${At}\:{the}\:{conclusion},{thanks}\:{for}\:{the}\:{key} \\ $$$${proof}. \\ $$
Commented by mr W last updated on 03/Mar/25
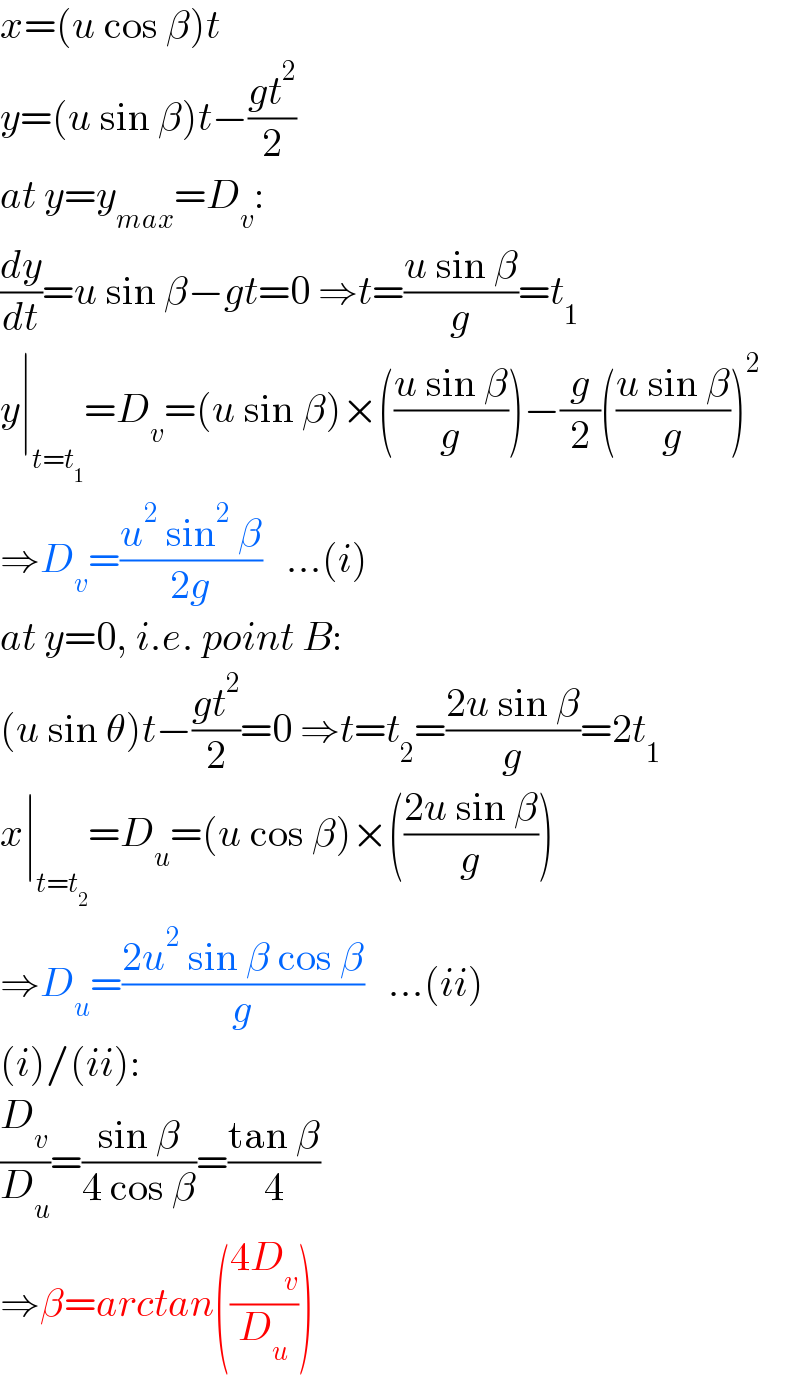
$${x}=\left({u}\:\mathrm{cos}\:\beta\right){t} \\ $$$${y}=\left({u}\:\mathrm{sin}\:\beta\right){t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${at}\:{y}={y}_{{max}} ={D}_{{v}} : \\ $$$$\frac{{dy}}{{dt}}={u}\:\mathrm{sin}\:\beta−{gt}=\mathrm{0}\:\Rightarrow{t}=\frac{{u}\:\mathrm{sin}\:\beta}{{g}}={t}_{\mathrm{1}} \\ $$$${y}\mid_{{t}={t}_{\mathrm{1}} } ={D}_{{v}} =\left({u}\:\mathrm{sin}\:\beta\right)×\left(\frac{{u}\:\mathrm{sin}\:\beta}{{g}}\right)−\frac{{g}}{\mathrm{2}}\left(\frac{{u}\:\mathrm{sin}\:\beta}{{g}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{D}_{{v}} =\frac{{u}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\beta}{\mathrm{2}{g}}\:\:\:...\left({i}\right) \\ $$$${at}\:{y}=\mathrm{0},\:{i}.{e}.\:{point}\:{B}: \\ $$$$\left({u}\:\mathrm{sin}\:\theta\right){t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0}\:\Rightarrow{t}={t}_{\mathrm{2}} =\frac{\mathrm{2}{u}\:\mathrm{sin}\:\beta}{{g}}=\mathrm{2}{t}_{\mathrm{1}} \\ $$$${x}\mid_{{t}={t}_{\mathrm{2}} } ={D}_{{u}} =\left({u}\:\mathrm{cos}\:\beta\right)×\left(\frac{\mathrm{2}{u}\:\mathrm{sin}\:\beta}{{g}}\right) \\ $$$$\Rightarrow{D}_{{u}} =\frac{\mathrm{2}{u}^{\mathrm{2}} \:\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta}{{g}}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\frac{{D}_{{v}} }{{D}_{{u}} }=\frac{\mathrm{sin}\:\beta}{\mathrm{4}\:\mathrm{cos}\:\beta}=\frac{\mathrm{tan}\:\beta}{\mathrm{4}} \\ $$$$\Rightarrow\beta={arctan}\left(\frac{\mathrm{4}{D}_{{v}} }{{D}_{{u}} }\right) \\ $$
