
Question Number 22051 by FilupS last updated on 10/Oct/17

$$\mathrm{I}\:\mathrm{have}\:\mathrm{recently}\:\mathrm{seen}\:\mathrm{a}\:\mathrm{different}\:\mathrm{notation} \\ $$$$\mathrm{for}\:\mathrm{integration},\:\mathrm{written}\:\mathrm{as}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int{dxf}\left({x}\right) \\ $$$${e}.{g}. \\ $$$$\:\:\:\:\:\:\int{dx}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\: \\ $$$$\mathrm{Is}\:\mathrm{this}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int{f}\left({x}\right){dx} \\ $$$$\Rightarrow\:\:\:\:=\int\left({x}+\mathrm{1}\right)^{\mathrm{2}} {dx} \\ $$$$??? \\ $$
Commented by Joel577 last updated on 10/Oct/17

$${I}\:{think}\:{it}\:{is}\:{same} \\ $$
Commented by Joel577 last updated on 10/Oct/17
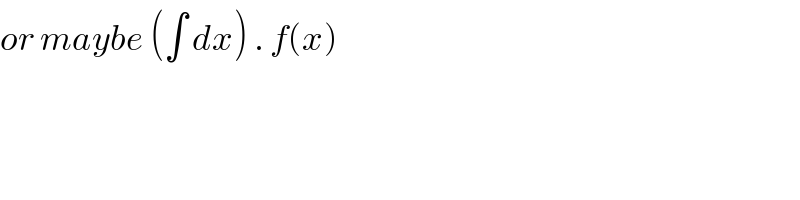
$${or}\:{maybe}\:\left(\int\:{dx}\right)\:.\:{f}\left({x}\right) \\ $$
Commented by FilupS last updated on 10/Oct/17

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{so}. \\ $$$$\mathrm{Without}\:\mathrm{going}\:\mathrm{into}\:\mathrm{details}, \\ $$$$\mathrm{they}\:\mathrm{got}\:\mathrm{something}\:\mathrm{in}\:\mathrm{form}: \\ $$$$\int{dxf}\left({x}\right)={F}\left({x}\right)+{c} \\ $$$$\: \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{am}\:\mathrm{only}\:\mathrm{aware}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form}: \\ $$$$\int{f}\left({x}\right){dx}={F}\left({x}\right)+{c} \\ $$$$\mathrm{to}\:\mathrm{me}:\:\int{dxf}\left({x}\right)=\left(\int{dx}\right)\left({f}\left({x}\right)\right) \\ $$$$\mathrm{whereas}:\:\int{f}\left({x}\right){dx}\neq\left(\int{dx}\right)\left({f}\left({x}\right)\right),\:\mathrm{because}: \\ $$$$\int{f}\left({x}\right){dx}=\left({F}\left({x}\right)\right)\left(\int{dx}\right) \\ $$
