
Question Number 4203 by Yozzii last updated on 01/Jan/16

$${I}\:{have}\:{no}\:{formal}\:{background}\:{in}\: \\ $$$${number}\:{theory},\:{but}\:{I}'{m}\:{curious} \\ $$$${of}\:{how}\:{to}\:{find}\:{positive}\:{integer}\:{solutions}\: \\ $$$$\left({x},{y},{z}\right)\:{to}\:{the}\:{equation}\:{x}^{{n}} +{y}^{{n}} ={z}^{{n}} \:{for}\: \\ $$$${n}\in\mathbb{Z}^{−} .\:{Fermat}'{s}\:{last}\:{theorem}\:{led} \\ $$$${me}\:{to}\:{this}.\:{Tell}\:{me}\:{about}\:{the}\:{cases} \\ $$$${of}\:{n}=−\mathrm{1},{n}=−\mathrm{2}\:{and}\:{n}=−\mathrm{3}. \\ $$
Commented by 123456 last updated on 01/Jan/16

$$\mathrm{what}\:\mathrm{if}\:{n}\in\mathbb{Q}? \\ $$
Commented by Rasheed Soomro last updated on 02/Jan/16
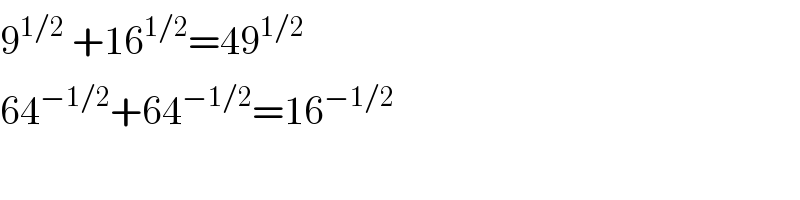
$$\mathrm{9}^{\mathrm{1}/\mathrm{2}} \:+\mathrm{16}^{\mathrm{1}/\mathrm{2}} =\mathrm{49}^{\mathrm{1}/\mathrm{2}} \\ $$$$\mathrm{64}^{−\mathrm{1}/\mathrm{2}} +\mathrm{64}^{−\mathrm{1}/\mathrm{2}} =\mathrm{16}^{−\mathrm{1}/\mathrm{2}} \\ $$
Answered by RasheedSindhi last updated on 01/Jan/16

$${Perhaps}\:{you}\:{are}\:{interesting}\:{in} \\ $$$${general}\:{solution},{not}\:{in}\:{individual}\: \\ $$$${solutions}! \\ $$$${I}'{ve}\:{attempt}\:{for}\:{individual}\:{ones}. \\ $$$${x}^{−\mathrm{1}} +{y}^{−\mathrm{1}} ={z}^{−\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\underset{} {{x}}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{1}}{{z}}\Rightarrow{yz}+{xz}={xy} \\ $$$${z}=\frac{{xy}}{{x}+{y}} \\ $$$${x}={y}=\mathrm{8} \\ $$$${z}=\frac{\mathrm{64}}{\mathrm{16}}=\mathrm{4} \\ $$$$−−−−−−−− \\ $$$${x}^{−\mathrm{2}} +{y}^{−\mathrm{2}} ={z}^{−\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{y}^{\mathrm{2}} }=\frac{\mathrm{1}}{{z}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} {z}^{\mathrm{2}} +{x}^{\mathrm{2}} {z}^{\mathrm{2}} ={x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} =\frac{{x}^{\mathrm{2}} {y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${x}={y}=\mathrm{4},{z}=\mathrm{8} \\ $$
Commented by Yozzii last updated on 01/Jan/16
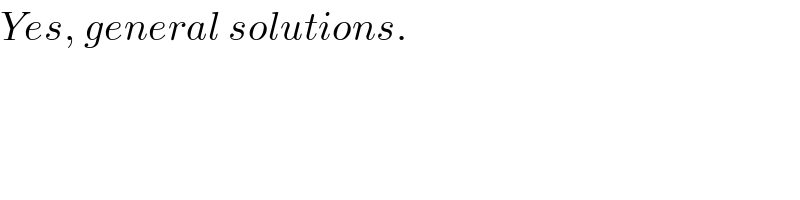
$${Yes},\:{general}\:{solutions}. \\ $$
Commented by Rasheed Soomro last updated on 01/Jan/16
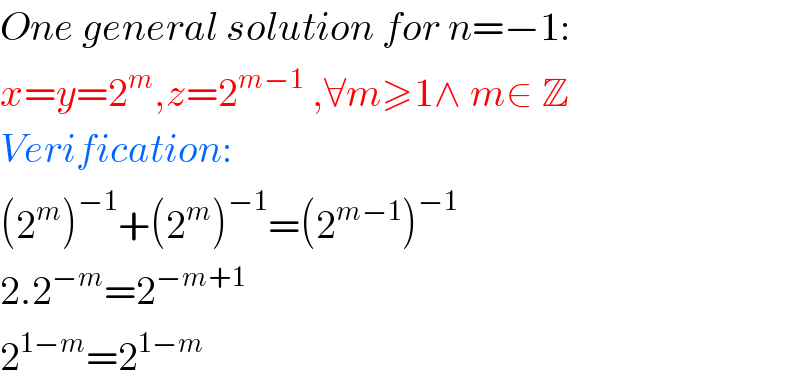
$${One}\:{general}\:{solution}\:{for}\:{n}=−\mathrm{1}: \\ $$$${x}={y}=\mathrm{2}^{{m}} ,{z}=\mathrm{2}^{{m}−\mathrm{1}} \:,\forall{m}\geqslant\mathrm{1}\wedge\:{m}\in\:\mathbb{Z} \\ $$$${Verification}: \\ $$$$\left(\mathrm{2}^{{m}} \right)^{−\mathrm{1}} +\left(\mathrm{2}^{{m}} \right)^{−\mathrm{1}} =\left(\mathrm{2}^{{m}−\mathrm{1}} \right)^{−\mathrm{1}} \\ $$$$\mathrm{2}.\mathrm{2}^{−{m}} =\mathrm{2}^{−{m}+\mathrm{1}} \\ $$$$\mathrm{2}^{\mathrm{1}−{m}} =\mathrm{2}^{\mathrm{1}−{m}} \\ $$
Commented by Yozzii last updated on 01/Jan/16
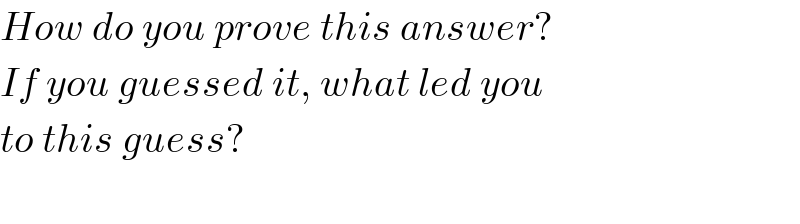
$${How}\:{do}\:{you}\:{prove}\:{this}\:{answer}? \\ $$$${If}\:{you}\:{guessed}\:{it},\:{what}\:{led}\:{you} \\ $$$${to}\:{this}\:{guess}?\: \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 01/Jan/16

$${x}^{−\mathrm{1}} +{y}^{−\mathrm{1}} ={z}^{−\mathrm{1}} \Rightarrow{z}=\frac{{xy}}{{x}+{y}} \\ $$$${z}\:{will}\:{be}\:{integer}\:{in}\:{case}\:{x}+{y}\:\mid\:{xy} \\ $$$${Assuming}\:{special}\:{case}\:{x}={y} \\ $$$${z}=\frac{{x}^{\mathrm{2}} }{{x}+{x}}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}}=\frac{{x}}{\mathrm{2}} \\ $$$${As}\:{z}\:{is}\:{integer}\:{so}\:\mathrm{2}\mid{x}\Rightarrow\:{x}\in\mathbb{E} \\ $$$${x}={y}=\mathrm{2}{k}\:{and}\:{z}={k}\:,\forall{k}\in\mathbb{N}\:\left(\boldsymbol{\mathrm{More}}\:\boldsymbol{\mathrm{simpler}}\:\boldsymbol{\mathrm{condition}}\right) \\ $$$${Verification}: \\ $$$$\left(\mathrm{2}{k}\right)^{−\mathrm{1}} +\left(\mathrm{2}{k}\right)^{−\mathrm{1}} ={k}^{−\mathrm{1}} \\ $$$$\mathrm{2}\left(\mathrm{2}{k}\right)^{−\mathrm{1}} ={k}^{−\mathrm{1}} \\ $$$$\left(\mathrm{2}.\mathrm{2}^{−\mathrm{1}} \right).{k}^{−\mathrm{1}} ={k}^{−} \\ $$$${k}^{−\mathrm{1}} ={k}^{−\mathrm{1}} \\ $$$$ \\ $$
Commented by Yozzii last updated on 01/Jan/16

$${Thank}\:{you}. \\ $$
Commented by Rasheed Soomro last updated on 01/Jan/16

$${Assuming}\:{special}\:{case} \\ $$$${y}=\mathrm{2}{x} \\ $$$${z}=\frac{{xy}}{{x}+{y}}\Rightarrow{z}=\frac{{x}.\mathrm{2}{x}}{{x}+\mathrm{2}{x}}=\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}{x}}=\frac{\mathrm{2}{x}}{\mathrm{3}} \\ $$$${z}\:{is}\:{integer}\:\Rightarrow\mathrm{3}\mid{x} \\ $$$${Hence}\:{Let}\:{x}=\mathrm{3}{k} \\ $$$${y}=\mathrm{2}\left(\mathrm{3}{k}\right)=\mathrm{6}{k} \\ $$$${z}=\frac{\mathrm{2}{x}}{\mathrm{3}}=\frac{\mathrm{2}\left(\mathrm{3}{k}\right)}{\mathrm{3}}=\mathrm{2}{k} \\ $$$$\left({x},{y},{z}\right)=\left(\mathrm{3}{k},\mathrm{6}{k},\mathrm{2}{k}\right) \\ $$$${Verification}: \\ $$$$\left(\mathrm{3}{k}\right)^{−\mathrm{1}} +\left(\mathrm{6}{k}\right)^{−\mathrm{1}} =\left(\mathrm{2}{k}\right)^{−\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}{k}}+\frac{\mathrm{1}}{\mathrm{6}{k}}=\frac{\mathrm{1}}{\mathrm{2}{k}}\Rightarrow\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}+\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 03/Jan/16
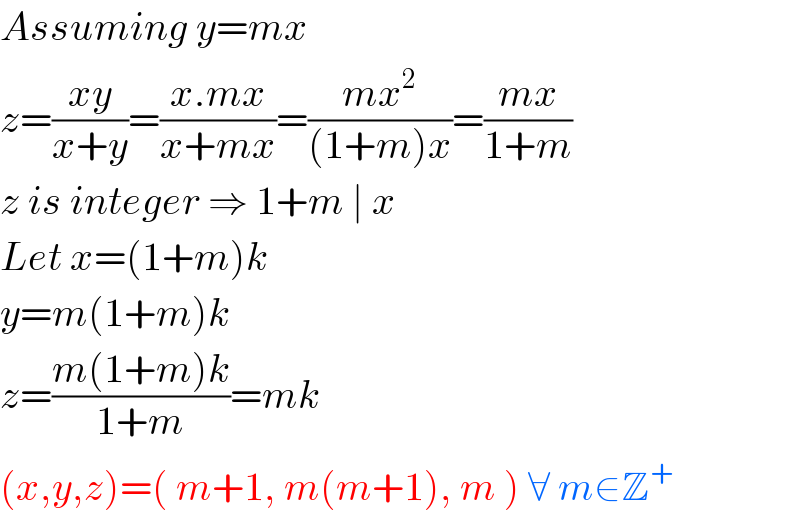
$${Assuming}\:{y}={mx} \\ $$$${z}=\frac{{xy}}{{x}+{y}}=\frac{{x}.{mx}}{{x}+{mx}}=\frac{{mx}^{\mathrm{2}} }{\left(\mathrm{1}+{m}\right){x}}=\frac{{mx}}{\mathrm{1}+{m}} \\ $$$${z}\:{is}\:{integer}\:\Rightarrow\:\mathrm{1}+{m}\:\mid\:{x} \\ $$$${Let}\:{x}=\left(\mathrm{1}+{m}\right){k} \\ $$$${y}={m}\left(\mathrm{1}+{m}\right){k} \\ $$$${z}=\frac{{m}\left(\mathrm{1}+{m}\right){k}}{\mathrm{1}+{m}}={mk} \\ $$$$\left({x},{y},{z}\right)=\left(\:{m}+\mathrm{1},\:{m}\left({m}+\mathrm{1}\right),\:{m}\:\right)\:\forall\:{m}\in\mathbb{Z}^{+} \\ $$
Commented by Rasheed Soomro last updated on 03/Jan/16
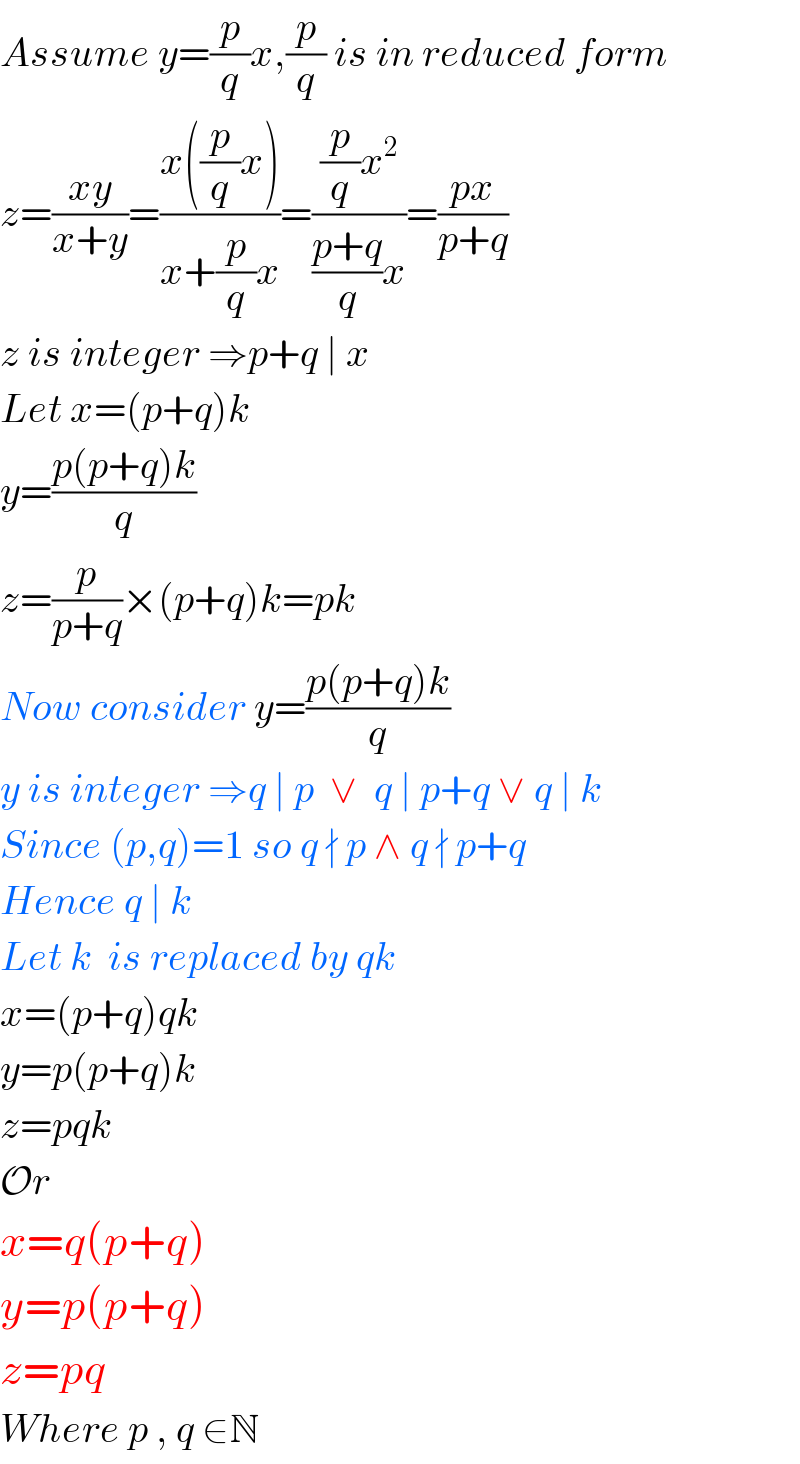
$${Assume}\:{y}=\frac{{p}}{{q}}{x},\frac{{p}}{{q}}\:{is}\:{in}\:{reduced}\:{form} \\ $$$${z}=\frac{{xy}}{{x}+{y}}=\frac{{x}\left(\frac{{p}}{{q}}{x}\right)}{{x}+\frac{{p}}{{q}}{x}}=\frac{\frac{{p}}{{q}}{x}^{\mathrm{2}} }{\frac{{p}+{q}}{{q}}{x}}=\frac{{px}}{{p}+{q}} \\ $$$${z}\:{is}\:{integer}\:\Rightarrow{p}+{q}\:\mid\:{x} \\ $$$${Let}\:{x}=\left({p}+{q}\right){k} \\ $$$${y}=\frac{{p}\left({p}+{q}\right){k}}{{q}} \\ $$$${z}=\frac{{p}}{{p}+{q}}×\left({p}+{q}\right){k}={pk} \\ $$$${Now}\:{consider}\:{y}=\frac{{p}\left({p}+{q}\right){k}}{{q}} \\ $$$${y}\:{is}\:{integer}\:\Rightarrow{q}\:\mid\:{p}\:\:\vee\:\:{q}\:\mid\:{p}+{q}\:\vee\:{q}\:\mid\:{k} \\ $$$${Since}\:\left({p},{q}\right)=\mathrm{1}\:{so}\:{q}\:\nmid\:{p}\:\wedge\:{q}\:\nmid\:{p}+{q} \\ $$$${Hence}\:{q}\:\mid\:{k} \\ $$$${Let}\:{k}\:\:{is}\:{replaced}\:{by}\:{qk} \\ $$$${x}=\left({p}+{q}\right){qk} \\ $$$${y}={p}\left({p}+{q}\right){k} \\ $$$${z}={pqk} \\ $$$$\mathcal{O}{r} \\ $$$${x}={q}\left({p}+{q}\right) \\ $$$${y}={p}\left({p}+{q}\right) \\ $$$${z}={pq} \\ $$$${Where}\:{p}\:,\:{q}\:\in\mathbb{N}\:\:\: \\ $$
Answered by 123456 last updated on 02/Jan/16

$$\mathrm{i}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{tha}\:\mathrm{fermat}\:\mathrm{theorem} \\ $$$$\mathrm{to}\:\mathrm{that} \\ $$$$\mathrm{by}\:\mathrm{fermat}\:\mathrm{last}\:\mathrm{theorem}\:\mathrm{there}\:\mathrm{no}\:\mathrm{other} \\ $$$$\mathrm{solution}\:\mathrm{than}\:\mathrm{the}\:\mathrm{trivials}\:\mathrm{one}\:\mathrm{to} \\ $$$${x}^{{n}} +{y}^{{n}} ={z}^{{n}} ,{n}\in\mathbb{N},{n}>\mathrm{2} \\ $$$$\mathrm{so}\:\mathrm{by}\:\mathrm{this}\:\mathrm{there}\:\mathrm{no}\:\mathrm{other}\:\mathrm{rational}\:\mathrm{solution}\:\mathrm{to} \\ $$$${x}^{{n}} +{y}^{{n}} ={z}^{{n}} \\ $$$$\mathrm{because}\:\mathrm{if}\:\mathrm{it}\:\mathrm{was} \\ $$$${x}=\frac{{p}_{{x}} }{{q}_{{x}} },{y}=\frac{{p}_{{y}} }{{q}_{{y}} },{z}=\frac{{p}_{{z}} }{{q}_{{z}} } \\ $$$${x}^{{n}} +{y}^{{n}} ={z}^{{n}} \\ $$$$\frac{{p}_{{x}} ^{{n}} }{{q}_{{x}} ^{{n}} }+\frac{{p}_{{y}} ^{{n}} }{{q}_{{y}} ^{{n}} }=\frac{{p}_{{z}} ^{{n}} }{{q}_{{z}} ^{{n}} } \\ $$$$\left({p}_{{x}} {q}_{{y}} {q}_{{z}} \right)^{{n}} +\left({q}_{{x}} {p}_{{y}} {q}_{{z}} \right)^{{n}} =\left({q}_{{x}} {q}_{{y}} {p}_{{z}} \right)^{{n}} \\ $$$${a}^{{n}} +{b}^{{n}} ={c}^{{n}} \\ $$$$\mathrm{and}\:\mathrm{note}\:\mathrm{that} \\ $$$${x}^{−{n}} =\frac{\mathrm{1}}{{x}^{{n}} }=\left(\frac{\mathrm{1}}{{x}}\right)^{{n}} ={a}^{{n}} \:\left(\mathrm{rational}\:\mathrm{solution}\right) \\ $$
