
Question Number 1592 by Rasheed Soomro last updated on 23/Aug/15

$$\mathrm{I}\:\mathrm{have}\:\mathrm{a}\:\mathrm{loop}\:\mathrm{of}\:\mathrm{string}\:\mathrm{of}\:\mathrm{length}\left(\mathrm{perimeter}\right)\:\:\mathrm{p}\:\mathrm{units}.\: \\ $$$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{make}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{of}\:\mathrm{largest}\:\mathrm{area}\:\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{loop}.\:\mathrm{What}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{dimensions}\:\mathrm{of}\:\mathrm{that}\:\mathrm{triangle}? \\ $$
Commented by 123456 last updated on 23/Aug/15
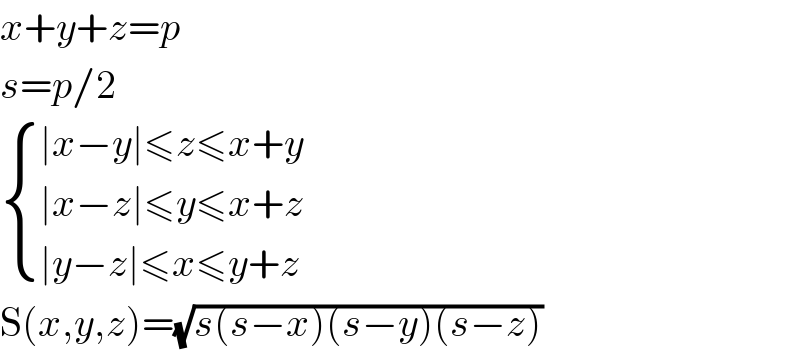
$${x}+{y}+{z}={p} \\ $$$${s}={p}/\mathrm{2} \\ $$$$\begin{cases}{\mid{x}−{y}\mid\leqslant{z}\leqslant{x}+{y}}\\{\mid{x}−{z}\mid\leqslant{y}\leqslant{x}+{z}}\\{\mid{y}−{z}\mid\leqslant{x}\leqslant{y}+{z}}\end{cases} \\ $$$$\mathrm{S}\left({x},{y},{z}\right)=\sqrt{{s}\left({s}−{x}\right)\left({s}−{y}\right)\left({s}−{z}\right)} \\ $$
Answered by prakash jain last updated on 10/Dec/15
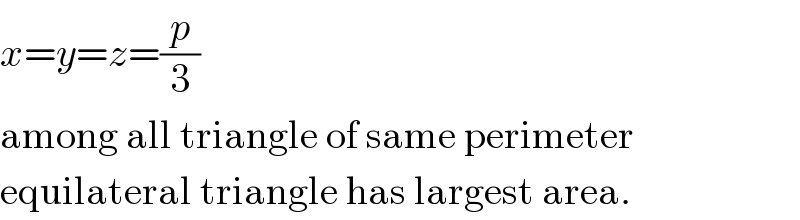
$${x}={y}={z}=\frac{{p}}{\mathrm{3}} \\ $$$$\mathrm{among}\:\mathrm{all}\:\mathrm{triangle}\:\mathrm{of}\:\mathrm{same}\:\mathrm{perimeter} \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{has}\:\mathrm{largest}\:\mathrm{area}. \\ $$
